系列收付款的现值和终值

系列收付款，是指不同时点上的若干笔资金。系列收付款的终值，是指现在不同时点上的若干笔资金在未来某一时点所对应的金额。系列收付款的现值，是指未来不同时点上的若干笔资金折算到现在所对应的金额。

（一）一般系列收付款的终值和现值

理解一般系列收付款终值和现值的计算，是理解年金终值和现值的基础。

1.一般系列收付款终值的计算

这个问题实际上就是将不同时点的资金逐一换算为未来某一时点的终值再求其合计的过程。它是一次性收付款现值求终值问题的发展，即分别将不同时点收付款的现值（当时值）按一定的利率（单利率或复利率）逐一换算为第n年末的终值，再将它们加起来，便得到系列收付款的终值。也就是说，系列收付款的终值就是每笔收付款的单利（复利）终值之和。

【例2-5】某人计划第1年初存款800元，第2年初存款1 000元，第3年初存款2 000元，第4年初存款1 000元，第5年初存款2 500元。假定年利率为10%。分别按单利和复利计算出5年末系列存款的本利和。

解：（1）若按单利计息，则第5年末系列存款的本利和为

F=800×（1+5×10%）+1 000×（1+4×10%）+2 000×（1+3×10%）+1 000×（1+2×10%）+2 500×（1+1×10%）=9 150（元）

（2）若按年复利计息，则第5年末系列存款的本利和为

F=800×（1+10%）5+1 000×（1+10%）4+2 000×（1+10%）3+1 000×（1+10%）2+2 500×（1+10%）

=800×1.610 5+1 000×1.464 1+2 000×1.331 0+1 000×1.210 0+2 500×1.1

=9 374.5（元）

2.一般系列收付款现值的计算

这个问题实质上是将不同时点的资金逐一换算为事前某一时点的现值再求其合计的过程。这是一次性收付款终值换算为现值问题的发展，只需将各期收付款额（当期终值）分别折算为期初（第0年）的现值，那么这些现值的合计数就是所求的系列收付款的现值。也就是说，系列收付款的现值就是每笔收付款的单利（复利）现值之和。

【例2-6】某人计划第1年初收款800元，第1年末收款1 000元，第3年初收款2 000元，第4年末收款2 500元。假定年利率为10%。分别按单利和复利计算出系列收款在第1年初的现值。

注意：在资金时间价值计算过程中，一定要区分年初和年末，如第3年初就是第2年末；碰到涉及年初的收付款项，建议画图帮助分析，横线代表时间的延续，用数字标出各期的顺序号；竖线的位置表示收付的时刻，竖线上端的数表示收付的金额。例2-6有关收款的形式如图2-1所示。

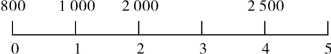
图2-1　例2-6有关收款的形式

解：（1）若按单利计息，则系列收款在第1年初的现值为

（2）若按年复利计息，则系列收款在第1年初的现值为

F=800+1 000×（1+10%）-1+2 000×（1+10%）-2+2 500×（1+10%）-4

=800+1 000×（P/F，10%，1）+2 000×（P/F，10%，2）+2 500×（P/F，10%，4）

=800+1 000×0.909 1+2 000×0.826 4+2 500×0.683 0

=5 069.4（元）

（二）特殊系列收付款的复利终值和现值——年金终值和现值

年金是指等额、定期的系列收付款项。例如，分期付款赊购、分期偿还贷款、发放养老金、分期支付工程款、每年相同的销售收入等，都属于年金收付形式。按照收付时点和方式的不同可以将年金分为普通年金、预付年金、递延年金和永续年金等四种。在年金中，系列等额收付的间隔期间只需要满足“相等”的条件即可，间隔时间可以不是一年，例如每季度等额支付的债务利息也是年金。

1.普通年金终值和现值

普通年金又称后付年金，是指各期期末收付的年金。普通年金的收付形式如图2-2所示。

图2-2　普通年金的收付形式

（1）普通年金终值的计算。

普通年金终值，就是一定时期内，在一定利率情况下，每期期末的等额收付款在整个期末的总价值，就是每期期末等额收付款项的复利终值之和。

设每期末的收付金额为A，利率为i，期数（或年金个数）为n，则普通年金终值的计算可用图2-3来说明。

图2-3　普通年金终值的计算示意图

由图2-3可以得出普通年金终值计算公式

式中，是普通年金算出终值的系数，称为年金终值系数，或称为1元的年金终值，用符号（F/A，i，n）表示。为了便于计算，可编制“年金终值系数表”（见附表三）备用。通过该表可查出，（P/A，10%，5）=6.101 5，其含义为：在年利率为10%的情况下，5年后的6.101 5元和1～5年每年年末的1元在经济上是等效的，根据这个系数可以把年金换算成终值。

【例2-7】如果1～5年每年末收付10 000元，利率为10%，则第5年末的终值为多少？

解：F=10 000×（F/A，10%，5）

=10 000×6.105 1

=61 051（元）

【例2-8】小王是位热心于公众事业的人，自2010年12月底开始，他每年都要向一位失学儿童捐款。小王向这位失学儿童每年捐款1 000元，帮助这位失学儿童从小学一年级读完九年义务教育。假设每年定期存款利率都是3%，则小王9年捐款在2019年年底相当于多少钱？

解：F=1 000×（F/A，3%，9）

=1 000×10.159

=10 159（元）

【例2-9】A矿业公司决定将其一处矿产的10年开采权公开拍卖，向世界各国煤炭企业招标开矿。已知甲公司和乙公司的投标书最具有竞争力，甲公司的投标书显示，如果该公司取得开采权，从获得开采权的第1年开始，每年年末向A公司交纳5亿元的开采费，直到10年后开采结束。乙公司的投标书表示，该公司在取得开采权时，直接付给A公司20亿元，在第8年末再付给30亿元。如A公司要求的年投资回报率达到15%，问应接受哪个公司的投标？

解：F甲=5×（F/A，15%，10）=5×20.304=101.52（亿元）

乙公司的方案对A公司来说是两笔收款，分别计算其终值：

第1笔收款（20亿元）的终值=20×（1+15%）10

=20×（F/P，15%，10）

=20×4.045 6

=80.912（亿元）

第2笔收款（30亿元）的终值=30×（1+15%）2

=30×（F/P，15%，2）

=30×1.322 5

=39.675（亿元）

F乙=80.912+39.675=120.578（亿元）

甲公司付出的款项终值小于乙公司付出的款项的终值，因此，A公司应接受乙公司的投标。

（2）偿债基金的计算。

偿债基金是指为使年金终值达到既定金额每期末应收付的年金数额。其实际上就是已知普通年金终值F，求年金A。

根据普通年金终值计算公式

可知

式中是普通年金终值系数的倒数，称偿债基金系数。它可以把普通年金终值折算为每期末应收付的年金数额。

【例2-10】拟在5年后还清10 000元债务，从现在起每年末等额存入银行一笔款项。假设银行存款利率为8%，每年需要存入多少元？

解：由于有利息因素，不必每年存入2 000元（10 000÷5），只要存入较少的金额，5年后本利和即可达到10 000元，可用以清偿债务。将有关数据代入上式

因此，在银行利率为10%时，每年存入1 705元，5年后可得10 000元，用来还清债务。

由以上分析可得结论：①普通年金终值和偿债基金，计算互为逆运算；②普通年金终值系数和偿债基金系数互为倒数。

（3）普通年金现值的计算。

普通年金现值，是指为在每期期末取得相等金额的款项而现在需要投入的金额。它是每次等额收付款项的复利现值之和。

设每期期末的取款金额为A，利率为i，期数（或年金个数）为n，则普通年金现值的计算可用图2-4来说明。

图2-4　普通年金现值的计算示意图

由图2-4可以得出普通年金现值计算公式

(www.xing528.com)

式中，是把普通年金算出现值的系数，称为年金现值系数，或称为1元的年金现值，用符号（P/A，i，n）表示。为了便于计算，可编制“年金现值系数表”（见本书附表四）备用。通过该表可查出，（P/A，10%，3）=2.486 9，其含义为：在年利率为10%的情况下，现在的2.486 9元和以后1～3年每年年末的1元在经济上是等效的，根据这个系数可以把年金换算成现值。

【例2-11】某人每年年末支付房租10 000元，共支付3年，设银行存款利率为10%，3年支付的所有房租相当于现在多少钱？

解：P=10 000×（1+10%）-1+10 000×（1+10%）-2+10 000×（1+10%）-3

=10 000×（P/A，10%，3）

=10 000×2.486 9

=24 869（元）

【例2-12】某投资项目于某年年初动工，假设当年投产，从投产之日起每年末可得收益10 000元。按年利率6%计算，计算预期10年收益的现值。

解：P=10 000×（P/A，6%，10）

=10 000×7.360 1

=73 601（元）

（4）资本回收额的计算。

资本回收额是指为使年金现值达到既定金额每期末应收付的年金数额。其实际上就是已知普通年金现值P，求年金A。

【例2-13】假设以10%的利率借款10 000元，投资于某个寿命为10年的项目，每年至少要收回多少现金才是有利的？

因此，每年至少要收回1 627元，才能还清贷款本利。

结论：①普通年金现值和资本回收额，计算互为逆运算；②普通年金现值系数和资本回收系数互为倒数。

2.预付年金终值和现值

预付年金是指在每期期初收付的年金，又称即付年金或先付年金。预付年金收付形式如图2-5所示。

图2-5　预付年金的收付形式

（1）预付年金终值计算。

n期预付年金与n期普通年金的付款次数相同，但由于付款时间的不同，n期预付年金终值（即n期预付年金在第n期末的价值）比n期普通年金终值多计算一次利息，或者说比n+1期普通年金终值少付最后一次款，所以，可根据普通年金终值公式来计算预付年金终值。预付年金终值的计算如下

式中，（F/A，i，n）（1+i）或（F/A，i，n+1）-1是预付年金终值系数，或称1元的预付年金终值。（F/A，i，n+1）-1和普通年金终值系数相比，期数加1，而系数减1，并可利用“年金终值系数表”查得（n+1）期的值，减去1后得出1元预付年金终值。

【例2-14】为给儿子上大学准备资金，王先生连续6年于每年年初存入银行3 000元。若银行存款利率为5%，则王先生在第6年末能一次取出本利和多少钱？

解：F=3 000×（F/A，5%，6）×（1+5%）

=3 000×6.801 9×（1+5%）

=21 426（元）

或者， F=3 000×[（F/A，5%，7）-1]

=3 000×（8.142 0-1）

=21 426（元）

（2）预付年金现值计算。

n期预付年金与n期普通年金的付款次数相同，但由于付款时间的不同，n期预付年金现值（即n期预付年金在0时点的价值）比n期普通年金现值少折现一次，也就是多计算一次利息，或者说比n-1期普通年金多一期不用贴现的付款A，所以，可根据普通年金现值公式来计算预付年金现值。预付年金现值的计算如下

式中，（P/A，i，n）（1+i）或（P/A，i，n-1）+1是预付年金现值系数，或称1元的预付年金现值。（P/A，i，n-1）+1和普通年金现值系数（P/A，i，n）相比，期数减1，而系数要加1，可利用“年金现值系数表”查得（n-1）期的值，然后加1，得出1元的预付年金现值。

【例2-15】6年分期付款购物，每年初付2 000元，设银行利率为10%，该项分期付款相当于一次现金收付的购价是多少？

解：P=A[（P/A，i，n-1）+1]

=2 000×[（P/A，10%，5）+1]

=2 000×（3.790 8+1）

=9 581.6（元）

或者， P=A（P/A，i，n）（1+i）

=2 000×（P/A，10%，6）×（1+10%）

=2 000×4.355 3×1.1

=9 581.66（元）

3.递延年金终值和现值

递延年金是指第一次收付发生在第二期或第二期以后的年金。递延年金的收付形式如图2-6所示。

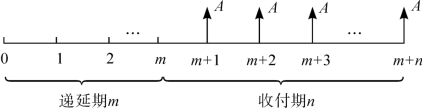
图2-6　递延年金的收付形式

从该图中可以看出，前m期没有发生收付。第一次收付在第m+1期期末，连续收付n次。

（1）递延年金终值计算。递延年金终值的计算方法和普通年金终值类似。前m期发生收付款的时期不计算，后面发生收付款的时期即n期，按n期普通年金计算递延年金终值即可。

【例2-16】某企业向银行借入一笔款项，银行贷款的年利率为10%，每年复利一次。银行规定前10年不用还本付息，但从第11年至第18年每年年末偿还10 000元。计算此系列款项的终值。

解：F=A（F/A，i，n）

=10 000×（F/A，10%，8）

=10 000×11.436

=114 360（元）

（2）递延年金现值计算。递延年金现值的计算方法有两种：

第一种方法，是把递延年金视为n期普通年金，求出递延期末（即图2-6中m期期末的位置）的现值，然后再将此现值调整到第一期期初（即图2-6中0的位置）。

第二种方法，是假设递延期中也进行收付，先求出（m+n）期的年金现值，然后，扣除实际并未收付的递延期（m）的年金现值，即可得出最终结果。

【例2-17】某企业向银行借入一笔款项，银行贷款的年利率为10%，每年复利一次。银行规定前10年不用还本付息，但从第11年至第18年每年年末偿还5 000元。要求：用两种方法计算这笔款项的现值。

解：第一种方法，

P=A×（P/A，10%，8）×（P/F，10%，10）

=5 000×5.334 9×0.385 5

=10 283.02（元）

第二种方法，

P=A×[（P/A，10%，18）-（P/A，10%，10）]

=5 000×（8.201 4-6.145）

=10 282（元）

4.永续年金终值和现值

无限期定额收付的年金，称为永续年金。现实中的存本取息，可视为永续年金的一个例子。

永续年金没有终止的时间，也就没有终值。永续年金的现值可以通过普通年金现值的计算公式导出

当n→∞时，（1+i）-n的极限为零，故上式可写成

【例2-18】拟建立一项永久性的奖学金，每年计划颁发10 000元奖金。若利率为5%，现在应存入多少钱？