消费者剩余与生产者剩余的分配问题

在完全竞争条件下某商品的需求函数为P＝113-Q2，供给函数为P＝（Q＋10）2，求消费者剩余和生产者剩余.

相关知识：消费者剩余；生产者剩余

需求是指在一定价格条件下，消费者愿意购买且有支付能力购买的商品量.设需求函数为P＝D（Q），这里Q为商品的需求量，P为该商品的价格，若该商品的市场价格为P0，相应的需求量为Q0，P0＝D（Q0），则原打算用高于市场价格P0的价格购买商品的消费者，会由于市场价格定于P0而得到好处，这个好处称为消费者剩余（即：愿意付出的金额-实际付出的金额），记作RD（Q0），即图1-6-6中阴影部分的面积.

类似地，生产者获得超过其生产成本的收益称为生产者剩余（即销售收益-生产成本），记作RS（Q0），即图1-6-7中阴影部分面积.

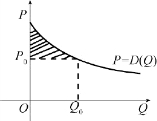
图1-6-6

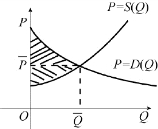
图1-6-8

问题1.6.5　解答

知识拓展

1.变上限积分函数

定义1.6.3　若函数f（x）在区间[a，b]上连续，那么在区间[a，b]上每一点x就有一个确定的定积分的值与x对应，即构成一个新的函数，称为积分上限函数或变上限定积分，记为Φ（x），即

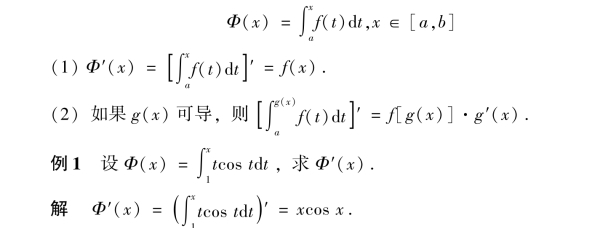
例7　求下列积分：

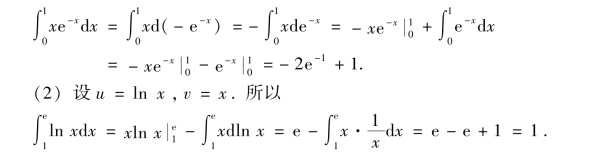
3.利用定积分求平面图形面积

一般地，如果函数y＝f（x），y＝g（x）在区间[a，b]上连续，并且在[a，b]上有g（x）≤f（x），则介于两条曲线y＝f（x），y＝g（x）以及两条直线x＝a，x＝b之间的平面图形的面积元素（见图1-6-9中的阴影部分）为dA＝[f（x）-g（x）]dx.因此，平面图形（见图1-6-9）的面积为

同样地，如果函数x＝φ（y），x＝ψ（y）在区间[c，d]上连续，并且在[c，d]上有φ（y）≤ψ（y），则介于两条曲线x＝φ（y），x＝ψ（y）以及两条直线y＝c，y＝d之间的平面图形（见图1-6-10）的面积元素为dA＝[ψ（y）-φ（y）]dy，因而此图形的面积为

图1-6-9

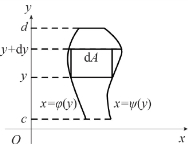
图1-6-10

例1　求曲线y＝ex，y＝e-x与直线x＝1所围成平面图形的面积.

解　如图1-6-12所示，先确定两条曲线交点的坐标.

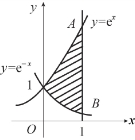
图1-6-11

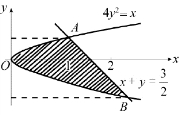
图1-6-12(www.xing528.com)

【基础练习1-6】

1.利用定积分的几何意义计算下列定积分：

【提高练习1-6】

【应用练习1-6】

2.【边际成本、边际收益与总利润】某厂生产某种产品Q单位时，边际成本为5元/单位，边际收益为10-0.02Q元/单位，当生产10单位产品时总成本为250元，问：生产多少单位产品时利润最大？并求出最大利润.

3.【纯收入贴现值】有一个大型的投资项目，投资成本为10 000万元，投资年利率为5%，每年的均匀收入率为2 000万元，求该无限期投资的纯收入贴现值.

4.【你能成为百万富翁吗？】某储户将10万元以活期存款形式存入银行，年利率为0.81%.

（1）如果以连续复利计算，在不计利息税的情况下，一年后储户可以得到多少本利和？

（2）按连续复利计算，该储户有可能成为百万富翁吗？

（3）如果该储户想在第10年成为百万富翁，他现在需存入多少钱？

6.【收入流的现值】设连续3年内每年有稳定的收入流15 000元，且年利率为7.5%，按连续复利计算其现值.

7.【收入流的现值与收回投资的年限】设某企业投资400万元，经测算，该企业在T＝10年中可以有稳定的收入流A（t）＝100万元，若年利率为10%，试求：

（1）该投资纯收入的现值；

（2）收回该投资的年限.

8.某商品的需求函数为P＝D（Q）＝24-3Q，供给函数P＝S（Q）＝2Q＋9，求市场均衡点及消费者剩余和生产者剩余.

【数学文化聚焦】微积分符号史漫谈

1.函数符号

1797年，拉格朗日大力推荐以f、F、φ及ψ表示函数，对后世影响深远.1820年，赫谢尔以f（x）表示x的函数.1839年，皮亚诺开始采用符号y＝f（x）及x＝f-1（y），成为现今通用的符号.

2.和式号

以“∑”来表示和式号是欧拉于1775年首先使用的，这个符号源于希腊文σογμαρω（增加）的字头，“∑”正是σ的大写.

3.极限符号

4.微分和导数符号

牛顿是最早以点号来表示导数的，他以v，x，y及z等表示变量，在其上加一点表示对时间的导数，如以x·表示x对时间的导数.此用法最早见于牛顿1665年的手稿.

5.积分符号

莱布尼兹于1675年以“omn·l”表示l的总和，而omn为“omnia”（意即所

【注释】

[1]1英里＝1.609 344千米.