设某产品在时刻t总产量的变化率为f(t)=100+12t-6t2(件/小时),求从t=2到t=4的总产量.
问题1.6.1 解答
分析:已知的总产量的变化率就是总产量的导数,要求从t=2到t=4的总产量就是求总产量函数的增加量.
先求总产量函数
![]()
则从t=2到t=4的总产量为
![]()
从上面的问题可以看出,已知导数求原函数,再通过原函数可以求出函数的增量是一个定值.也就是已知导数可以求得函数的增量是定值,这个就是定积分的问题.如果用定积分的方法来求,那么应用范围会更广、更具普遍性和更加简便.
相关知识:定积分的概念与计算;定积分的几何意义和经济意义

1.定积分的概念
由区间[a,b]上的连续曲线y=f(x)(f(x)≥0),x轴与直线x=a,x=b所围成的平面图形称为曲边梯形(见图1-6-1).
由于曲边梯形底边上各点处的高f(x)在区间[a,b]上是变动的,因此不能利用已有的面积公式求出面积.为计算曲边梯形AabB的面积,可按下述方法进行:
(1)分割.用任意的n-1个分点a=x0<x1<…<xn-1<xn=b把区间[a,b]分成n个小区间:[x0,x1],[x1,x2],…,[xn-1,xn],其中第i个小区间长度为Δxi=xi-xi-1(i=1,2,…,n).
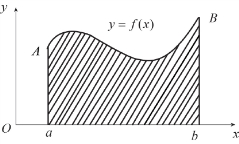
图1-6-1
过每一分点xi(i=1,2,…,n-1)作x轴的垂线,把曲边梯形AabB分成n个小曲边梯形,其中第i个小曲边梯形的面积记为ΔAi(见图1-6-2).曲边梯形AabB的面积A等于n个小区间的面积之和,即
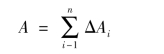
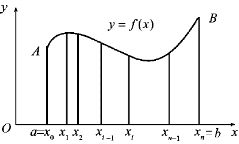
图1-6-2
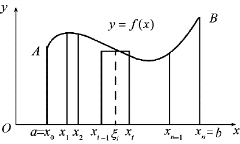
图1-6-3
(2)近似.在每一小区间[xi-1,xi]上任取一点ξi(i=1,2,…,n),以Δxi为底边、f(ξi)为高作小矩作,其面积为f(ξi)Δxi(i=1,2,…,n)(见图1-6-3).
当Δxi很小时ΔAi≈f(ξi)Δxi.
(3)求和.把这n个小曲边梯形的面积的近似值加起来,便得到曲边梯形AabB的面积近似值,即

定义1.6.1 设函数f(x)在区间[a,b]上有定义.用点a=x0<x1<x2<…<xn-1<xn=b,把区间[a,b]任意分为n个小区间:
 (https://www.xing528.com)
(https://www.xing528.com)
![]()

2.定积分的几何意义
显然从上面曲边梯形的面积可看出定积分的几何意义:


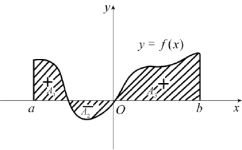
图1-6-4
3.定积分的性质
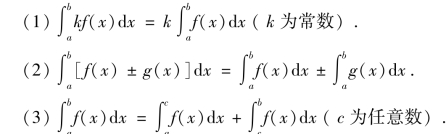
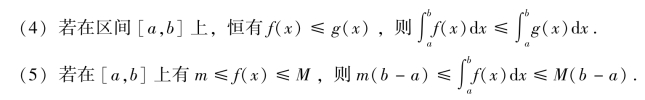

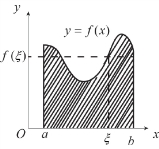
图1-6-5
4.定积分计算公式——牛顿—莱布尼茨公式(微积分基本定理)
设f(x)在区间[a,b]上连续,F(x)是f(x)的一个原函数,则
![]()
这样,求定积分就是先求原函数,然后把上、下限代入原函数,再把所得的函数值相减即可.
问题1.6.1 解答(定积分法)
从t=2到t=4的总产量为
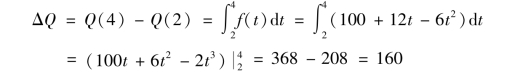

5.定积分的经济意义

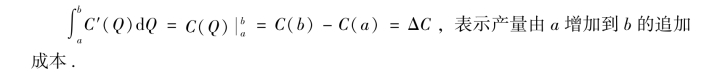


免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




