利润函数推导：通过边际利润计算

某商品的边际利润函数为L′（Q）＝6Q-Q2，Q为该商品的销售量，销售此商品的盈亏平衡点为Q＝3，求总利润函数.

问题1.5.6　解答

边际利润和利润的关系是导数与原函数的关系，由边际利润求利润函数为

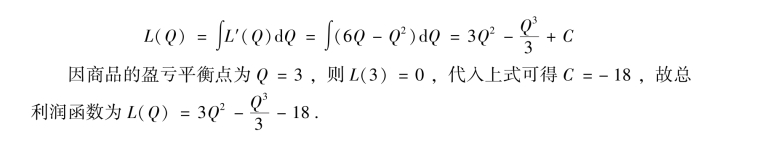
类似地，有以下常用关系.

边际成本与成本、边际收入和收入、边际利润和利润的关系都是导数与原函数的关系：

知识拓展：不定积分的计算方法

1.直接积分法

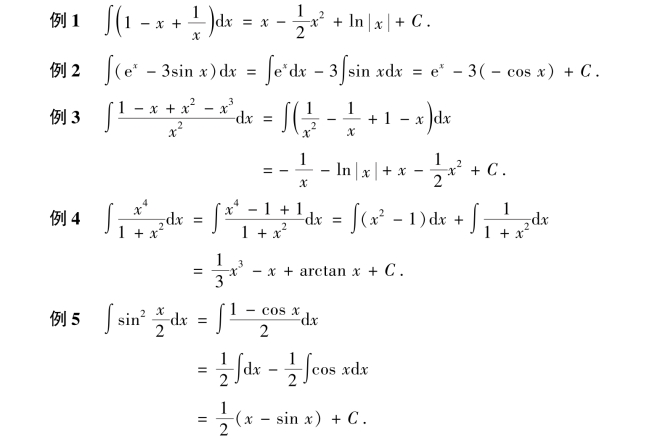
注：当不定积分不能直接应用基本积分表和不定积分的性质进行计算时，需先将被积函数化简或变形再进行计算.计算的结果是否正确，只需对结果求导，看其导数是否等于被积函数.

2.凑微分积分法（第一类换元法）

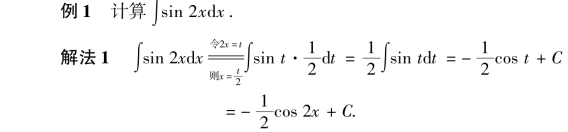
3.换元积分法（换元去根号）

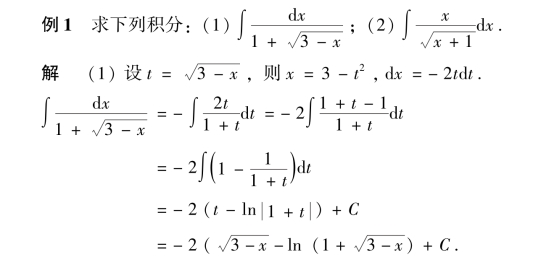
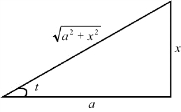
图1-5-1

4.分部积分法

在使用分部积分时，正确地选择u和dv是关键.选择u和dv的原则是：①v容易求得；②积分∫vdu容易求出.一般选u的规律为：最先考虑反三角函数或对数函数，其次考虑幂函数，最后考虑三角函数或指数函数.

【基础练习1-5】

1.验证函数F（x）＝x（ln x-1）是f（x）＝ln x的一个原函数.

2.求下列不定积分：

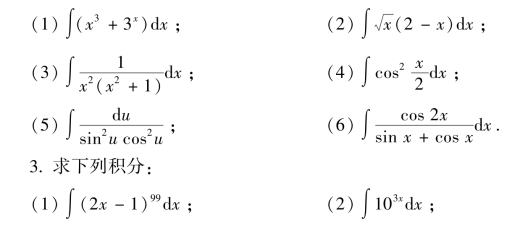
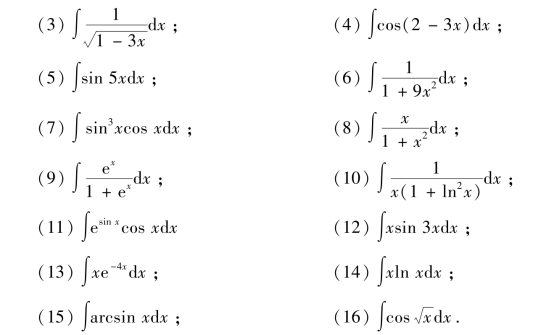
【提高练习1-5】

1.设函数f（x）的一个原函数为sin 2x，则∫f′（2x）dx＝（　）.(www.xing528.com)

【应用练习1-5】

1.【边际成本、平均成本与总成本】设某产品生产q个单位的总成本函数为C（q）＝1 000＋0.012q2（元）

求：（1）生产1 000件产品时的总成本和平均成本；

（2）生产1 000件产品时的边际成本.

2.【边际收入、平均收入与总收入】设生产某种产品q个单位时的收入为R（q）＝200q-0.01q2，求生产50个单位产品时的收入、单位产品的平均收入及边际收入.

4.【边际需求】某商品的需求函数为Q（p）＝75-p2，求p＝4时的边际需求，并说明其经济含义.

6.【边际需求、需求弹性、总收益】商品的需求量Q为价格p的函数Q（p）＝150-2p2.

（1）确定p＝6时的边际需求，并说明其经济意义；

（2）确定p＝6时的需求弹性，并说明其经济意义；

（3）当p＝6时，若价格下降1%，总收益将变化百分之几？是增加还是减少？

7.【边际收益与收益的弹性】某商品的总收益R关于销量Q的函数R（Q）＝104Q-0.4Q2，求：

（1）销量为Q时的边际收入；

（2）销量Q＝50时的边际收入；

（3）销量Q＝100时的总收入R对Q的弹性.

8.【需求弹性与边际收益】已知销售某商品的总收益（R＝pQ）的函数为R＝60Q-Q2，计算需求弹性为-2时的边际收益.

9.【边际收益与收益函数】设某商品的边际收益函数为R′（Q）＝10-5Q，求收益函数.

10.【产品变化率与产量函数】已知某产品产量对时间的变化率是时间t的函数Q′（t）＝0.2t＋1，设此产品在时间t的产量为Q（t），且Q（0）＝0，求Q（t）.

11.【成本与成本函数】设某工厂生产q单位产品的总成本C是q的函数，已知边际成本为C′（q）＝25＋30q-9q2，固定成本是55元，求总成本与产量的函数关系式.

12.【边际成本、边际收入与利润函数】某种产品每天生产Q台时的固定成本为80元，边际成本为C′（Q）＝0.6Q＋20（元/台），边际收益为R′（Q）＝32（元/台），求利润函数.

【数学文化聚焦】李大潜院士谈学数学的目的

许多在实际工作中成功地应用数学并取得相当突出成绩的数学系毕业生都有这样的体会：在工作中真要用到的具体数学分支学科，具体的数学定理、公式和结论，其实并不很多，学校里学过的很多知识似乎没有派上什么用处，但所受的数学训练，所领会的数学思想和精神，却无时无刻不在发挥着积极的作用，成为取得成功的最重要的因素.因此，如果仅仅将数学作为知识来学习，而忽略了数学思想对学生的熏陶以及学生数学素质的提高，就失去了开设数学课程的意义.

实际上，严格的数学训练，可以使学生具备一些特有的素质，这些素质包括：

（1）可以使学生树立明确的数量观念，“胸中有数”，认真地注意事物的数量方面及其变化规律.

（2）提高学生的逻辑思维能力，使他们思路清晰、条理分明、有条不紊地处理头绪纷繁的各项工作.

（3）数学上的推导要求每一个正负号、每一个小数点都不能含糊敷衍，有助于培养学生认真细致、一丝不苟的作风.

（4）数学上追求的是最有用（广泛）的结论、最低的条件（代价）以及最简明的证明，可以使学生形成精益求精的风格.

（5）使学生知道数学概念、方法和理论的产生和发展的渊源和过程，了解和领会由实际需要出发到建立数学模型，再到解决实际问题的全过程，提高他们运用数学知识处理现实世界中各种复杂问题的意识、信念和能力.

（6）可以使学生增强拼搏精神和应变能力，能通过不断分析矛盾，从表面上一团乱麻的困难局面中理出头绪，最终解决问题.

（7）可以调动学生的探索精神和创造力，使他们更加灵活和主动，在改善所学的数学结论、改进证明的思路和方法、发现不同的数学领域或结论之间的内在联系、拓展数学知识的应用范围以及解决现实问题等方面，逐步显露出自己的聪明才智.

（8）使学生具有某种数学上的直觉和想象力，包括几何直观能力，能够根据所面对的问题的本质或特点，八九不离十地估计到可能的结论，为实际的需要提供借鉴.

数学教育本质上是一种素质教育，使学生不仅知道许多重要的数学概念、方法和结论，而且领会到数学的精神实质和思想方法，这应该是数学教育努力追求的目标，也是衡量数学教学的成效与优劣的最根本的依据.