是否值得投资？考虑这些要素

设一笔10 000元投资可以用3年，第1年提供的收益为5 000元，第2年提供的收益为4 000元，第3年提供的收益为2 000元.

（1）如果年利率为6%，则这笔投资所提供的未来三年中收益的现值是多少？是否值得投资？

（2）如果年利率为4%，则这笔投资所提供的未来三年中收益的现值是多少？是否值得投资？

分析：这里是否值得投资需要看净现值（收益现值-投资成本）.厂商进行某项投资的净现值代表了该项投资对厂商价值或股东财富的贡献.净现值是否为正值成为投资决策规则，即净现值大于零则值得投资；净现值小于零则不值得投资.

问题1.2.4　解答

这时，净现值＝收益总现值-投资成本＝9 956-10 000＝-46（元）＜0，不值得投资.也就是说，这10 000元投资带来的三年总收益折算成的现值只有9 956元，低于原来的投资价值，即当初只需投资9 956元就可以获得同样多的收益，所以这个投资是不值得的.

（2）若投资A0＝10 000，年利率为r＝0.04，则未来三年提供的收益的现值分别为

则这笔投资所提供的未来三年总收益的现值为A0＝A1＋A2＋A3＝10 284（元）.这时，净现值＝收益总现值-投资成本＝10 284-10 000＝284（元）＞0，值得投资.也就是说，这10 000元投资带来的三年总收益折算成的现值有10 284元，高于原来的投资价值，所以这个投资是值得的.

知识拓展

1.常见极限类型及解法

在以后的学习中，例3、例6的结果可以作为公式使用，在这两个例子中，用正切函数任意替换正弦函数，结果仍成立.

例7　求下列函数的极限：

2.函数的连续性

定义1.2.5　设函数y＝f（x）在点x0的某个领域内有定义，如果当x→x0时，函数f（x）的极限存在且等于f（x）在点x0处的函数值f（x0），即

则称函数y＝f（x）在点x0连续.否则称函数y＝f（x）在点x0处间断，并称x0为函数的间断点.

若函数y＝f（x）在区间（a，b）内每一点都连续，则称函数y＝f（x）在区间（a，b）内连续.若函数y＝f（x）在区间（a，b）内连续，且它在左端点a处右连续，在右端点b处左连续，则称函数y＝f（x）在闭区间[a，b]上连续.（即函数y＝f（x）在区间[a，b]上的图像是一条连绵不断的曲线.）

基本初等函数在其定义域内连续.初等函数在其定义区间内是连续的.

（2）因为初等函数在其定义区间内都是连续的，所以当x＜0时，函数f（x）＝x-1是连续的；当x＞0时，函数f（x）＝x＋1是连续的；虽然f（x）在x＝0处有定义f（0）＝0，但

即f（x）在x＝0处左、右极限不相等，所以f（x）在x＝0处极限不存在.因此x＝0是f（x）的间断点.

3.闭区间上连续函数的性质

闭区间上的连续函数具有一些重要性质.现在，我们将这些性质列在下面.从几何上看，这些性质都是十分明显的，但是要严格证明它们，还需要其他知识，在这我们就不加以证明了.

性质1（具有最大（最小）值）　闭区间[a，b]上的连续函数f（x）在[a，b]上必有最大值和最小值.即在[a，b]上，至少有两个点x1和x2，使得对[a，b]上的一切x，有

这里f（x1）和f（x2）分别是f（x）在[a，b]上的最小值m＝f（x1）和最大值M＝f（x2）.（见图1-2-1）

性质2（零点存在定理）　若f（x）在[a，b]上连续，且f（a）和f（b）异号，则至少存在一点ξ∈（a，b），使得f（ξ）＝0（见图1-2-2）

性质3（介值定理）　闭区间[a，b]上的连续函数f（x）可以取其最小值和最大值之间的一切值.即设f（x）在[a，b]上的最小值为m，最大值为M，那么，对于任何c：m＜c＜M，至少存在一点ξ∈（a，b），使得f（ξ）＝c.（见图1-2-3）

图1-2-1

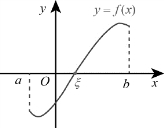
图1-2-2(www.xing528.com)

图1-2-3

【基础练习1-2】

1.判断下列数列的敛散性：

3.求下列极限：

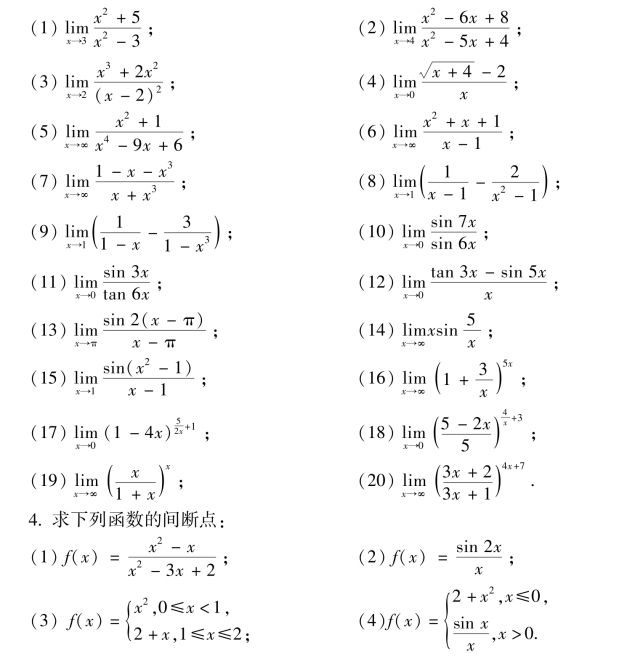
【提高练习1-2】

A.无穷大量　B.无穷小量

C.有界变量　D.无界变量

5.函数y＝f（x）在点x0处有定义是函数y＝f（x）在点x0处有极限的（　）.

A.充分条件　B.必要条件

C.充要条件　D.既不充分也不必要条件

6.函数y＝f（x）在点x0处有定义是函数y＝f（x）在点x0处连续的（　）.

A.充分条件　B.必要条件

C.充要条件　D.既不充分也不必要条件

【应用练习1-2】

1.【理财收益】某人用100万元购买年报酬率为20%的股票，分别以按年结算和连续复利结算两种方式计算5年和10年后的收益.

2.【还款问题】某人用分期付款的方式从银行贷款50万元用于购买商品房，设贷款期限为10年，年利率为4%.按连续复利计算，10年末还款的本利和为多少？

3.【销售预测】推出一种新的电子游戏光盘时，在短期内销售量会迅速增加，然后下降，其函数关系为，试对该产品的长期销售作出预测.

4.【利息问题】设本金为1万元，年利率为10%，存款1年.（1）按复利计算；（2）按连续复利计算.1年后的本利和各为多少？

5.【哪一种投资方案合算】某人有1万元，想进行投资，现有两种投资方案：

（1）一种是一年支付一次红利，年利率是12%；

（2）另一种是一年分12个月按复利支付红利，月利率1%，哪一种投资方案合算？

（3）若另按连续复利支付红利又是多少？

6.【贷款还款总额】某医院2000年5月20日从美国进口一台彩色超声波诊断仪，贷款20万美元，以复利计息，年利率4%，2009年5月20日到期一次还本付息，试确定贷款到期时还款总额.

（1）若一年计息2期；

（2）若按连续复利计息.

7.【传染病传染的人数】假定某种传染病流行t天后，感染的人数由下式给出

问：（1）如果不加控制，从长远考虑，将有多少人感染上这种病？

（2）有可能到某天为止，共有100万人染上这种病吗？50万人呢？25万人呢？

【数学文化聚焦】祖冲之与圆周率

祖冲之（429—500年），我国南北朝时期的伟大科学家、数学家，自幼受家庭书墨熏陶，酷爱天文与数学.他天资聪颖，勤奋好学，除了汲取古籍精华之外，又亲身观测实验.史书上记载他“亲量圭尺，躬查仪漏，目尽毫厘，心穷筹策.”

在生产应用方面，祖冲之改造了指南车，制作了水碓磨、千里船、漏钟等.他兴趣广泛，才华横溢，在哲学、文学、音乐等方面均有很深的造诣，曾注释《易经》《论语》等，还撰写小说《述异记》十卷.

祖冲之的杰出成就是世界科学史上的光辉篇章，他的伟大贡献备受后人瞩目，月球上发现的重要山脉中有“祖冲之山”，以纪念这位伟大的中国科学家.