设某小区二室一厅商品房价值1 000 000元,李某自筹了400 000元,要购房还需贷款600 000元,贷款月利率为0.5%,条件是每月还一些,25年内还清,假如还不起,房子归债权人.问:李某具有什么能力才能贷款购房呢?
问题0.3 分析与解答
分析:起始贷款600 000元,贷款月利率r=0.005,贷款n月=25×12=300月,每月还x元,yn表示第n个月仍欠债主的钱.
建立模型:y0=600 000
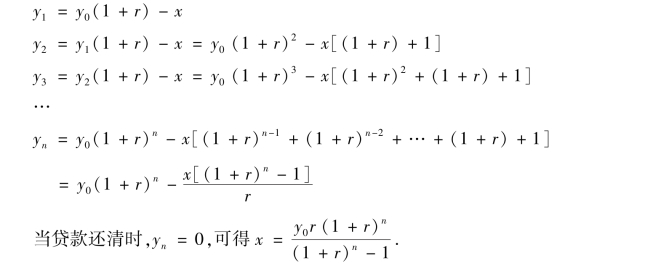
把n=300,r=0.005,y0=600 000代入得x≈3 865.8,即李某如不具备每月还款3 866元的能力,就不能贷款.
知识拓展
函数在数学建模中常常被应用,高等数学是以函数为主要研究对象的一门数学课程,所以我们有必要来回顾复习一下学过的主要函数.
1.基本初等函数
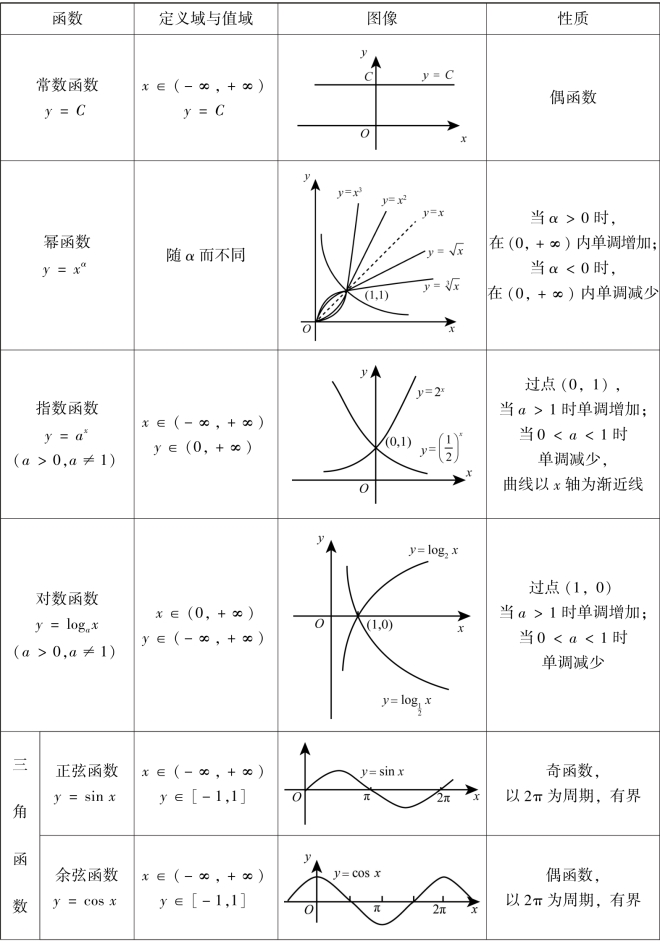
我们将已学过的常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数.它们的定义域、值域、图像和性质如表0-2所示.
表0-2
续表
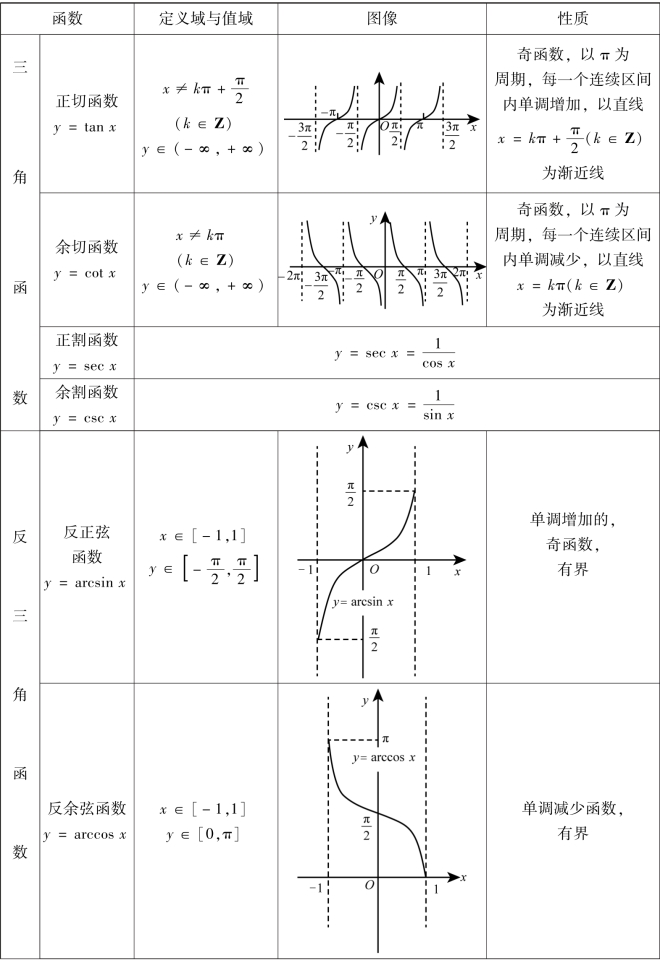
续表
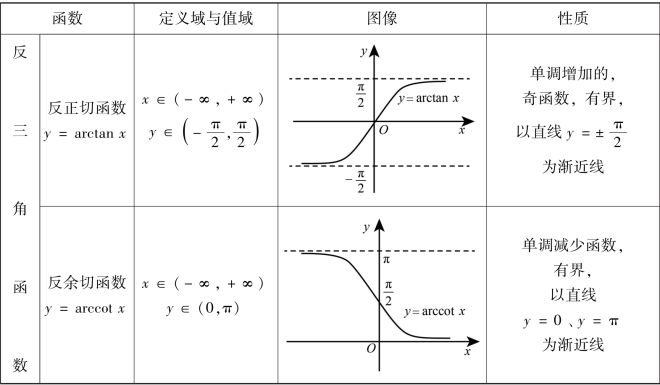
2.复合函数
设y是u的函数y=f(u),u是x的函数u=φ(x).如果u=φ(x)的值域或其部分包含在y=f(u)的定义域中,则y通过中间变量u构成x的函数,称为x的复合函数,记作
![]()
其中,x是自变量,u称作中间变量.
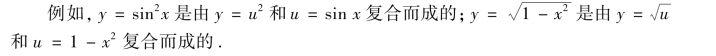

要认识复合函数的结构,必须要认识其复合过程,也要理解复合函数如何进行分解.通常采取由外层到内层分解的办法,将y=f[φ(x)]拆成若干基本初等函数或简单函数的复合.习惯上,我们将基本初等函数经过有限次四则运算所得到的函数称为简单函数.
复合函数分解为简单函数的步骤:
第一步:确定外层函数y=f(u)(y是u的函数);
第二步:确定内层函数u=φ(x)(u是x的函数).
复合函数分解为简单函数的标准:
(1)基本初等函数(幂函数、指数函数、对数函数、三角函数及反三角函数);
(2)基本初等函数的四则运算;
(3)特别注意多项式函数,如一次多项式函数ax+b,二次多项式函数ax2+bx+c等.
例1 指出下列函数的复合过程:
(1)y=sin(x3+4); (2)y=5sin x2.
解(1)设u=x3+4,则y=sin(x3+4)由y=sin u,u=x3+4复合而成.
(2)设u=sin x2,则y=5u;设v=x2,则u=sin v,所以,y=5sin x2可以看成是由y=5u,u=sin v,v=x2三个函数复合而成的.
例2 设f(x)=x3,g(x)=ln x,求(1)f[g(x)];(2)g[f(x)].
解 f(x)=x3定义域为R,g(x)=ln x定义域为(0,+∞),
它们的交集非空,因而可以复合.
(1)f[g(x)]=[g(x)]3=(ln x)3=ln3 x;
(2)g[f(x)]=ln[f(x)]=ln x3.(https://www.xing528.com)
3.初等函数
由基本初等函数经过有限次的四则运算及有限次的复合而成的函数叫作初等函数.一般来说,初等函数都可以用一个解析式子表示.
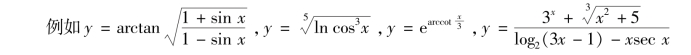
都是初等函数.而
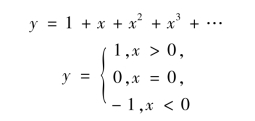
都不是初等函数.
4.函数的几种特性
(1)单调性:设函数y=f(x)在区间(a,b)内有定义,如果对于(a,b)内的任意两点x1和x2,当x1<x2时,有f(x1)<f(x2)(或f(x1)>f(x2)),则称函数f(x)在(a,b)内是单调增加(或单调减少)的.单调增加函数与单调减少函数统称为单调函数.
单调增加函数的图形沿x轴的正向上升,单调减少函数的图形沿x轴的正向下降.(见图0-2)
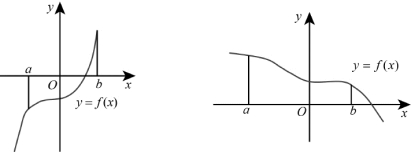
图0-2
(2)奇偶性:设函数y=f(x)在集合D上有定义,如果对任意的x∈D,恒有f(-x)=f(x)(或f(-x)=-f(x)),则称f(x)为偶函数(或奇函数).
偶函数的图形关于y轴对称;奇函数的图形关于原点对称.(见图0-3)
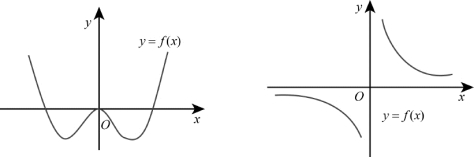
图0-3
(3)周期性:对于函数y=f(x),如果存在非零常数T,使f(x)=f(x+T)恒成立,则称此函数为周期函数.T称为周期.
若T为函数y=f(x)的周期,则kT(k∈Z)也是函数y=f(x)的周期.我们把满足f(x)=f(x+T)的最小正数T0称为最小正周期.
周期函数的图形每经过一个周期T重复出现一次.

函数y=f(x)在区间(a,b)内有界的几何意义是:曲线y=f(x)在区间(a,b)内被限制在两条平行于x轴的直线y=M与y=N之间,如图0-4所示.
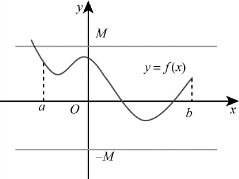
图0-4
注:


【应用练习0-1】
1.【快递邮费】某快递公司规定:寄送到某地的物件,当物件不超过20千克时,按基本邮费每千克3元计算;当超过20千克时,超过部分按每千克4.5元计算.试求寄送到该地的物件的邮费y(元)与物件重量x(千克)之间的函数关系.
2.【乘坐出租车收费问题】某城市出租汽车收费情况如下:起价10元(4千米以内),行程不足15千米,大于等于4千米部分,每公里车费1.6元;行程大于等于15千米部分,每公里车费2.4元,计价器每0.5千米计一次价.建立车费与行程的函数关系式.若分别行驶12千米和23.7千米,分别应付多少车费?
3.【租车费用】A汽车租赁公司的某款汽车每天租金为200元,每千米附加费为1.2元.B汽车租赁公司提供的同款汽车每天租金为250元,每千米附加费为0.8元,问:(1)分别写出两家公司出租一天这款汽车的费用与行驶里程的函数关系;(2)在同一坐标系上画出这两个函数的图像;(3)租哪一家公司的车比较合算?
4.【人民币和美元兑换】小林住在美国,有一次她想去加拿大旅游,就把人民币兑换成了加元,币面数值增加了12%.后来因故未去成,于是她又把加元兑换成美元,这时币面数值减少了12%.问:小林亏了还是赚了?亏或赚了多少?
5.【公寓出租的最大利润】某房地产公司有50套公寓要出租.当租金定为每月500元时,公寓会全部租出去;当月租金增加20元时,就有一套公寓租不出去,而租出去的房子每月要花费60元的维护费.试问:房租定为多少可获最大收入?
6.【贷款和分期付款】叶同学了解到:某数码城对笔记本电脑进行分期付款销售.每台售价为4 000元的笔记本电脑,如果分36个月付款,每月只需付150元.同时来自银行的贷款信息为:5 000元以下的贷款,在3年内还清,年利率为15%.那么,他应该向银行贷款还是分期付款来购得这种笔记本电脑?
【数学文化聚焦】数学模型与求解实际问题的描述
数学家在数学建模的第一阶段并没有起到明显的作用,起作用的通常是研究这类问题的科学家、工程师、医生,甚至是企业家,正是这些人认识到了问题的重要性和与数学方法的可结合性,近年来,数学的应用已引起广泛的注意,因此,往往在提出系统的理论以前,有关数据的收集,经验性的结论已完成,所缺少的是数学家的介入.一旦有数学家介入,问题将会发生质的变化.
第二阶段是整个建模过程中最困难又最关键的部分.它最富有创造性,由具有数学知识的科学家参与,或由数学家与科学家共同参与,模型的建立由仔细地理解问题,区分主次和选取合适的数学结构所组成.模型有两个方面:一方面是数学结构;另一方面是实际概念与数学结构间的对应.基于对同一问题的观察和研究提出的数学模型可能有几种不同的数学结构.不同的数学结构可能反映问题的不同侧面,例如,光的物理模型有两个:一个是波动说;一个是粒子说,它们都是有用的.
第三个阶段是求解数学问题.这个阶段的研究在表面上与纯数学的研究没有区别,只是动机不同而已,然而,数学问题与实际问题有密切的联系,这是很重要的一点.
第四阶段是计算.为了加深对原问题的理解,计算是必不可少的,但是,由于实际问题的复杂性,大部分的计算结果不能借助手工来完成,因此算法的研究以及计算机的使用是必须的.
第五阶段是依照原问题去解释和评价所得结果.这时可能出现各种情况,我们需要针对不同的情况作出详细分析,而分析的结论则能推动我们去进一步完善模型.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




