数学建模：跨越各领域的函数模型

随着科学技术的进步，数学的应用已不再局限于自然科学，它已大量应用于经济学、管理学、信息科学、环境科学等各个领域，大到国民经济，小到公司管理、个人规划等均离不开数学这个工具.许多以定性为基础的学科正逐步走上定量化的道路.数学在搞好经济管理、发展生产以及自然学科或社会学科中的重要性已为越来越多的人所认识.通过本部分的学习，学生将初步了解数学建模的过程和方法，领略如何用数学来描述自然现象、社会现象的变化规律，并用它来解决问题.

数学模型是针对现实世界的某一特定对象，为了一个特定的目的，根据特有的内在规律，作出必要的简化和假设，运用适当的数学工具，采用形式化语言，概括或近似地表述出来的一种数学结构.它能解释特定对象的现实状态，或能预测特定对象的未来状态，或能提供处理特定对象的最优决策或控制.函数关系可以看作一种变量间有相互依存关系的数学模型.通过举例，了解如何运用学过的函数解决一些简单的实际例子，从而初步了解建立数学模型的过程.学好数学最有效的学习方法是通过数学模型方法去认识基本的实际问题.数学模型方法如图0-1所示.

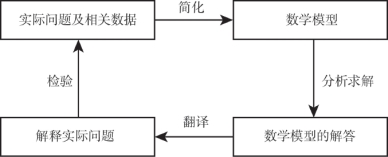
图0-1

数学模型的构建和解决实际问题的步骤分为以下五个阶段：(www.xing528.com)

（1）科学地识别与剖析实际问题；

（2）形成数学模型（分析问题中哪些是变量，哪些是常量，分别用不同的字母表示；根据所给的条件，运用相关知识，确定一个满足这些关系的函数或图形）；

（3）求解数学模型；

（4）研究算法，并尽量使用计算机；

（5）回到实际中去，解释结果.