一元线性回归分析方法简介

7.3.1 回归分析的概念与特点

7.3.1.1 回归分析的概念

“回归”一词是英国生物学家高尔顿(Francis Galton，1822—1911年)首先提出的。高尔顿在研究父母亲身高和子女身高的关系时发现: 身材特别高的父母所生的孩子其身材并非特别高，而身材特别矮的父母所生孩子的身材也并非特别矮，子辈身高有向父辈平均身高逼近的趋向，他把这种现象叫做“身高数值从一极端至另一极端的回归”。以后，高尔顿的学生皮尔逊(Pearson，1857—1936年)把回归的概念同数学的方法联系起来，把代表现象之间一般数量关系的统计模型叫做回归直线或回归曲线，从此诞生了统计学中著名的回归理论。后来，回归这个词被用来泛指变量之间的一般数量关系。

现象之间的相关关系，虽然不是严格的函数关系，但现象之间的一般关系值可以通过函数关系的近似表达式来反映，这种表达式根据相关现象的实际对应资料，运用数学的方法来建立，这类数学方法称回归分析。即根据现象之间相关关系的形式，配合一条最适合的直线或曲线(本章只介绍直线)，用这条直线反映它们之间数量变化的一般关系，即当自变量发生一个量的变化时，因变量一般会(或平均会)发生多大量的变化。例如，单位面积化肥施用量增加一公斤，稻谷单产量会增产多少公斤。反映现象间相关关系数量变化规律的这条直线，就叫回归直线，表现这条回归直线的数学表达式，称直线回归模型，它是推算或预测因变量的经验数据模型。直线回归模型有一元线性回归模型(只反映两个现象之间的相关关系)和多元线性回归模型(反映三个或三个以上现象之间的相关关系)。本章仅讨论一元线性回归模型。

7.3.1.2 回归分析的特点

(1)回归分析的两个变量是非对等关系。相关分析中，相关关系的两个变量是对等的，不必区分哪一个是自变量，哪一个是因变量。而回归分析中，两个变量是因果关系，需要确定哪个是因变量，哪个是自变量。自变量、因变量不同，所得出的分析结果也不同。

(2回归分析中，因变量是随机变量，自变量是可控制变量。在回归分析中，可依研究的目的分别建立y对于x的回归方程或x对于y的回归方程; 而相关分析中，被研究的两个变量都是随机变量，它只能计算出反映两个变量之间相关密切程度的一个统计分析指标——相关系数。

(3)相关分析是回归分析的基础，回归分析是相关分析的深入和继续。只有当两个变量间存在高度相关时，进行回归分析才有意义。

7.3.1.3 回归分析的内容

回归分析是指将具有相关关系的现象的变量转变为函数关系，并建立变量关系的数学表达式，来研究变量之间数量变动关系的统计分析方法。具体内容包括两个方面:

(1)确定现象之间相关关系的数学模型。

回归分析的目的之一就是根据一个现象的变动对另一现象的变动作出数量上的判断，测定变量间的一般数量变化关系。即建立描述现象间相关关系的数学模型——回归方程，用函数关系式近似地表现相关关系，进而找出现象间相互依存关系数量上的规律性，作为判断、推算、预测的根据。

(2)测定数学模型的拟合精度。

数学模型是现象间相关与回归关系的数量描述形式，模型拟合的精度，直接影响着统计分析结论的准确性。因此，在模型建立后，需要对其精确度进行检验。统计上一般通过计算估计标准误差来测定。估计标准误差小，说明模型的拟合精度高，从而进行统计分析结论的可靠性就大; 反之，估计标准误差大，说明模型的拟合精度低，则统计分析结论的可靠性就低。

7.3.2 一元线性回归模型

一元线性回归模型是用来进行两个变量间回归分析的。回归分析的重要内容之一，就是根据变量观测值构建回归直线方程，对现象间存在的一般数量关系进行描述。

7.3.2.1 构建回归模型应具备的条件

(1)现象间确实存在数量上的相互依存关系。只有当两个变量存在高度密切的相关关系时，所构建的回归模型才有意义，用其进行分析和预测才有价值。

(2)现象间存在直线相关关系。一元线性回归方程在图形上表现为一条直线，因此，只有当两个变量的相关关系表现为直线相关时，所配合的直线方程才是对客观现象的真实描述，才可用来进行统计分析。如果现象间的相关关系表现为曲线，却配合为一条直线，这必然会得出错误的分析结论。实际中，一般是借助散点图来判定现象是否呈直线相关。

(3)具备一定数量的变量观测值。回归直线方程是根据自变量和因变量的样本观测值求得的，因此，变量x和变量y两者应有一定的数量的对应观测值，这是构建直线方程的依据。如果观测太少，受随机因素的影响较大，就不易观察现象间的变动规律性，所求出的直线回归方程也就没有多大意义了。

7.3.2.2 直线回归方程的求法

直线回归方程又称一元一次线性回归方程，若以x表示自变量，y表示因变量，则其基本形式为:

式中:为回归估计值。

模型中的参数a、b与直线趋势方程相同，通常用最小平方法来求。最小平方法的数学出发点是:

令G(a，b) =∑(y-a-bx)2，根据高等数学中求极值的原理:

即:

这就是求解参数a、b的二元一次方程组。解之即求得a、b的公式如下:

这里，b为回归系数，它表示自变量x每增加一个单位时，因变量y的平均增减量，b ＞0为增量，b ＜0为减量。b的符号与相关系数r的符号一致。若r＞0，则b＞0，变量呈正相关;若r ＜0，则b ＜0，变量呈负相关。

［例7.3］某公司连续10年每年广告费与年销售收入的数据见表7-5，请建立回归方程。

表7-5 某公司A产品广告费与销售收入相关表

解: 设年广告费为自变量x，年销售收入因变量y，则有:

y =a+bx

一元线性回归方程计算表见表7-6。

依据表7-6数据可得:

表7-6 一元线性回归方程计算表

一元线性回归方程为:

y =48.2143+1.1429x

方程中a=48.2143为初始水平，b =1.1429为回归系数。方程表明年广告费每增加1万元，年销售收入将会增加1.1429万元。

在SPSS中，相关分析主要通过【Analyze】—【Regression】—【Linear】来实现，如例7.3，在SPSS中录入数据，结果见表7-7。

表7-7 回归分析结果(www.xing528.com)

a.Dependent Variable: 年销售收入

据表7-7，例7.3的结果为y=48.214+1.143x

同理，用例7.3也可做变量的相关分析，录入数据，结果见表7-8。

表7-8 Pearson相关系数

＊＊.Correlation is significant at the 0.01 level(2-tailed).

表7-8给出Pearson相关系数及其显著性检验结果，相关系数为0.955，相关系数的Sig. 为0，小于0.05，说明年广告费与年销售收入的相关性是显著的。

7.3.3 一元回归模型的检验

7.3.3.1 相关系数及其显著性检验

一般来说，相关系数可以反映自变量x和因变量y之间的线性相关程度，相关系数r的绝对值越接近于1，则x与y之间的线性关系越密切。相关系数通常是根据总体的样本数据计算得出，带有一定的随机性，会出现误差，因而有必要对相关系数进行显著性检验，以此来说明建立的回归模型有无实际意义。

为保证回归方程具有最低的线性关系，人们将相关系数r的临界值列成专门的表，即相关系数检验表。按给定的显著性水平α值以及自由度n，查相关系数检验表，即可找到对应的r的最低临界值rα，据此就可以判断线性关系是否成立。在社会经济现象中显著性水平α通常取0.05(95%以上建立的回归模型方才可靠、精确)。自由度指的是样本容量n与回归模型中待定参数的个数m之间的差，即自由度 =n-m。如例7.3中样本容量n=10，回归模型中待定参数个数m=2，则自由度=n-m=10-2=8。若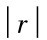≥rα(n-m) ，表明在显著性水平α条件下，变量间的线性关系是显著的，建立的回归方程是有意义的; 若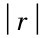＜rα(n-m)，表明在显著性水平α条件下变量间的线性关系不显著，建立的回归模型实际意义待定。

［例7.4］依据例7.3的资料，对A产品年广告费及年销售收入的相关关系进行显著性检验。

解: 由表7-8可知，r =0.955，自由度 =n-m =10-2 =8，给定α =0.05，查相关系数检验表得r0.05(10-2)=0.6319。r＞r0.05(10-2)，表明有95%的概率保证A产品年广告费与年销售收入之间具有线性相关关系，所建立的回归方程y=48.2143+1.1429x是有意义的。

7.3.3.2 估计标准误差检验

估计标准误差也称为估计标准差或估计标准误，是残差平方和的算术平均数的平方根，用Sy表示。其计算公式为:

式中:Sy代表估计标准误差;ei代表估计残差(实际值与估计值之差);n代表样本容量;m代表回归模型中待定参数的个数;。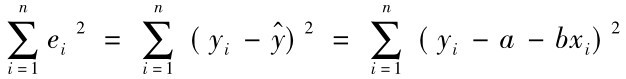

残差的平方和可以反映出实际值与回归直线的离散程度，而计算其平均数，可以消除求和项数对残差平方和的影响。因而，在此基础上计算出的估计标准误差更能反映出实际值与回归直线的平均离散程度。估计标准差是一项误差分析指标，用于判断回归模型拟合的优劣程度。

上式计算估计标准差较繁琐，可以采用简捷计算方法计算估计标准差。其简捷计算公式为:

［例7.5］运用表7-6中的数据计算估计标准差。

解:由表7-6可知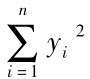，=28885，a=48.2143，b=1.1429，=537，n=10 ，m=2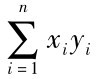，=2616，则用简捷公式计算估计标准差:

Sy越大，实际值与回归直线的离散程度越大; 反之，Sy越小，实际值与回归直线的离散程度越小。一般要求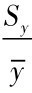＜15%。

运用上述两种公式计算出的估计标准差从理论上说应该是相等的，但在实际计算过程中，由于回归方程的待定系数a和b也是利用公式计算出来的，在计算的过程中通常会涉及四舍五入的情况，所以两种计算公式的结果会出现不一致，但其偏差往往很小，不会影响对问题的分析。

上例中Sy=0.7154，=53.7，=0.0133。

由此可见，一元线性回归方程y =48.2143+1.1429x的精度较好。

7.3.3.3 运用模型进行预测

一元线性回归模型通过上述检验，若其精度较好，拟合度优，即可用其进行预测。如例7.3中一元线性回归方程y =48.2143+1.1429x，若2012年A产品广告费为8万元，将x =8(万元)代入回归方程中，则2013年销售收入预测值为:

y =48.2143+1.1429×8=57.3575(万元)

由于实际计算中不可避免要出现误差，预测值应该是在一定的范围之内的一个数值，而不是一个确定值。因此，除了测算一个数值点外，还应测算预测值可能产生的范围，即测算其置信区间。上述预测只测算了一个数值点，假定其他因素不变，Sy=0.7154，置信度为95%( F(t)=95%)，查正态分布概率表，F(t) =95%，t=1.96，则A产品2005年估计销售收入为:

即A产品年广告费为8万元时，其年销售收入在55.9553万～58.7597万元。

7.3.3.4 应用相关分析与回归分析应注意的问题

相关分析与回归分析都是重要的统计分析方法，在统计学知识体系中占有重要的地位。它们对于人们加深现象间相互依存关系的认识，促使这种认识由定性阶段进入定量阶段都具有重要意义。但是，应该看到，相关分析和回归分析与其他统计方法一样，也有自己的局限性，因此，在实践中应注意如下几方面的问题:

(1)注意定性分析与定量分析的结合。

相关分析是分析社会经济现象之间相关关系的，相关系数的计算、回归方程的建立都是基于现象间所固有的客观联系之上的。而现象之间是否一定存在相关关系，主要是靠定性分析，即依据社会经济理论、专业知识、实际经验对事物进行分析来判定的。不通过定性分析，直接根据样本观测数据进行量化分析、构建模型，有时就可能得出错误的结论。因为任何两列数据，即使是毫不相关的两个现象，都可以计算出相关系数，构建出回归模型。因此，相关分析中的一切量化分析都应建立在定性分析基础之上。

(2)注意客观现象质的规定性。

现象间所存在的相互依存关系都是有一定数量界限的。例如，一般来说，施肥量越多，粮食产量越高，但是超过一定的限度，施肥量增加，粮食产量可能反而下降。同样，固定资产投资与国民经济发展速度的关系也是有一个数量界限的。也就是说，某些现象之间的相关关系在一定的限度内是正相关，而超过某一界限，则可能是负相关，在一定限度内是直线相关，而在另一界限内可能是曲线相关。如果进行统计分析时不加区别，不注意现象间质的数量界限，就可能影响统计分析结论的可信度。

(3)注意社会经济现象的复杂性。

客观社会经济现象间彼此有着千丝万缕的联系，某一现象发生的原因，有可能是另一现象出现的结果。而且，有时某一事件的出现可能导致诸多事件的发生，产生一系列的连锁反应。因此，进行统计分析时，要充分考虑现象间的复杂性，注意偶然和个别因素的影响，这样才能保证统计分析的质量。

(4)注意对相关系数和回归直线方程的有效性进行检验。

应该注意，相关分析中所得出的回归系数、回归直线方程、估计标准误差等都是根据样本数据求得的，但所作的结论却是对总体的。例如，由30个人的身高与体重值计算出相关系数为0.95，所作出的结论并不是说30个人的身高与体重存在着相关关系，而是说人的身高与体重具有相关关系。显然，这里存在一个由样本代表总体的问题。因此，使用相关系数、回归模型进行统计分析时，要对其有效性进行检验。