如何分析简单线性相关关系？

7.2.1 相关关系的一般判断

进行相关关系分析，首先要判断现象间是否存在相关关系。判断现象间是否存在相关关系，一般是对现象进行定性分析和绘制相关图。

7.2.1.1 定性分析

对现象进行定性分析，就是根据现象质的规定性，运用理论知识、专业知识、实际经验来进行判断和分析。例如，根据经济理论，来判别居民的货币收入与社会商品购买力是否存在相关关系; 根据生物遗传理论，来判别父辈的身高与子辈的身高是否存在相关关系，等等。定性分析是进行相关分析的基础，在此基础上，根据需要通过编制相关表和绘制相关图来进行分析。

7.2.1.2 相关表

相关表是一种反映变量之间相关关系的统计表。将某一变量按其取值的大小排列，然后再将与其相关的另一变量的对应值平行排列，便可得到简单的相关表。

［例7.1］对某10户居民家庭的年可支配收入和消费支出进行调查，得到的原始资料见表7-1。请编制相关表。

表7-1 居民年收入和消费水平调查资料 单位: 千元

解: 根据调查原始资料，将可支配收入按从小到大顺序排列，可编制出相关表，见表7-2。

表7-2 居民年收入和消费水平相关表 单位: 千元

从相关表中可以看出，随着居民收入水平的提高，消费水平也相应提高，两者之间存在明显的正相关关系。

7.2.1.3 相关图

相关图也叫相关散点图，它是根据相关表中的观测数据在坐标图中所绘制的点状图形。用x和y分别代表两个变量，把相关表中的对应观测值一一描绘在坐标图中，则形成了反映相关点分布状况的图形，据此就可以观测现象间相关关系的情况，如根据表7-2的数据绘制的相关图见图7-1。

图7-1

在相关图中，若相关点呈现出一定的规律性，如大致为一条直线，表明现象间存在相关关系，且为直线相关或曲线相关。相关点越密集，表明相关关系越密切。若相关点分布毫无规律，表明现象间无相关关系或存在低度的相关关系。社会经济现象之间的相关，多数属直线相关。因此，直线相关分析在实际中最为常用。受篇幅所限，在此只讲直线相关分析。直线相关关系的密切程度是通过直线相关系数来度量的。

7.2.2 相关系数的含义及检验

7.2.2.1 相关系数的含义

相关系数是指直线相关条件下，说明两现象之间相关关系密切程度的统计分析指标，用r表示。其定义公式为:

式中: r表示相关系数; x表示自变量; y表示因变量; xi表示自变量及其变量值; yi表示因变量及其变量值; 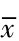为自变量数列的平均值; 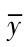为因变量数列的平均值。

该公式也可写成:

式中:r表示简单相关系数;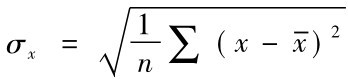代表自变量的标准差;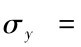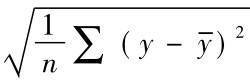代表因变量的标准差;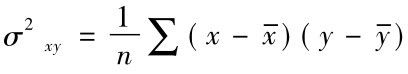代表自变量x与因变量y的协方差。(www.xing528.com)

由此可知，相关系数是两个变量协方差与两个变量标准差乘积的比。

依相关系数的定义公式可知相关系数的含义如下:

(1)r的取值范围为: -1≤r≤1。因为协方差的绝对值最小为0，最大为σx和σy的乘积。

(2)r的绝对值越接近于1，表明相关关系越密切; 越接近于0，表明相关关系越不密切。

(3)r=1或r=-1，表明两现象完全相关。

(4)r=0，表明两变量无直线相关关系。

(5)r＞0，表明现象呈正直线相关; r＜0，表明现象呈负直线相关。实际中| r| ＜0.3视为无相关; 0.3≤| r| ＜0.5为低度相关; 0.5≤| r| ＜0.8为显著相关; | r| ≥0.8称为高度相关。

7.2.2.2 相关系数的计算

根据相关系数的定义公式可直接计算相关系数。具体计算时，要使用相关表资料设计一个计算表，将公式中所需要的基本数据先计算出来，即需要列出5个计算栏: 。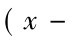

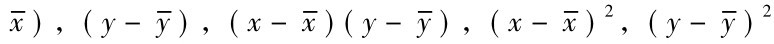相关系数的计算公式:

［例7.2］根据表7-2的资料，计算居民年可支配收入(x)与消费支出(y)之间的相关系数。

解: 相关系数计算表见表7-3。

表7-3 相关系数计算表

将表中计算结果代入公式可得:

计算结果说明居民的消费支出与可支配收入之间存在着高度的相关关系。

在SPSS中，相关分析主要通过【Analyze】—【Correlate】—【Bivariate】来实现，如例7.2，在SPSS中录入数据，结果如表7-4所示。

表7-4 Pearson相关系数

＊＊.Correlation is significant at the 0.01 level(2-tailed).

表7-4给出Pearson相关系数及其显著性检验结果，其相关系数为0.988，相关系数的Sig. 为0，小于0.05，说明可支配收入与消费支出的相关性是显著的。