5.1.1 抽样调查
5.1.1.1 抽样调查的概念
抽样调查的概念有广义和狭义两种理解。按照广义的理解,凡是抽取一部分单位进行观察,并根据观察结果来推断全体的都是抽样调查,其中又可分为非随机抽样和随机抽样两种。非随机抽样就是由调查者根据自己的认识和判断,选取若干个有代表性的单位,根据这些单位进行观察的结果来推断全体,如民意测验等。随机抽样则是根据大数定律的要求,在抽取调查单位时,应保证总体中各个单位都有同样的机会被抽中。一般所讲的抽样调查,大多数是指这种随机抽样而言,即狭义的抽样调查。所以,严格意义上的抽样调查就是: 按照随机原则从总体中抽取一部分单位进行观察,并运用数理统计的原理,以被抽取的那部分单位的数量特征为代表,对总体做出数量上的推断分析。
5.1.1.2 抽样调查的特点
(1)和全面调查相比较,抽样调查能节省人力、费用和时间,而且比较灵活。
抽样调查的调查单位比全面调查少得多,因而既能节约人力、费用和时间,又能比较快地得到调查的结果,这对许多工作都是很有利的。例如,农产量全面调查的统计数字要等收割完毕以后一段时间才能得到,而抽样调查的统计数字在收获的同时就可以得到,一般能早得到两个月左右,这对于安排农产品的收购、储存、运输等都是很有利的。
由于调查单位少,有时可以增加调查内容。因此,有的国家在人口普查的同时也进行人口抽样调查,一般项目通过普查取得资料,另一些项目则通过抽样调查取得资料。这样既可以节省调查费用和时间,又可以丰富调查内容。
(2)有些情况下,抽样调查的结果比全面调查要准确。
统计数字与客观实际数量之间是会有差别的,这种差别通常称为误差。统计误差有两种: 一是登记误差,也叫调查误差或工作误差,是指在调查登记、汇总计算过程中发生的误差,这种误差应该设法避免; 二是代表性误差,这是指用部分单位的统计数字为代表,去推算总体的全面数字时所产生的误差,这种误差一定会发生,是不可避免的。
全面调查只有登记误差而没有代表性误差,而抽样调查则两种误差全有。因此,人们往往认为抽样调查不如全面调查准确,这种看法忽略了两种误差的大小。全面调查的调查单位多,涉及面广,参加调查汇总的人员也多,水平不齐,因而发生登记误差的可能性就大。抽样调查的调查单位少,参加调查汇总的人员也少,可以进行严格的培训,因而发生登记误差的可能性就小。在这种情况下,抽样调查的结果会比全面调查的结果更为准确。
(3)抽选部分单位时要遵循随机原则。
其他非全面调查,如典型调查和重点调查等,一般是要根据统计调查任务的要求,有意识地选取若干个调查单位进行调查,而抽样调查不同,从总体中抽取部分单位时,必须非常客观,毫无偏见,也就是严格按照随机原则抽取调查单位,不受调查人员任何主观意图的影响,否则会带上个人偏见,挑中那部分单位的标志值可能偏高或偏低,失去对总体数量特征的代表性。
(4)抽样调查会产生抽样误差,抽样误差可以计算,并且可以加以控制。
在非全面调查方式中,典型调查固然也可用它所取得的部分单位的数量特征去推算全体的数量特征,但这种推算的误差范围和保证程度,是无法事先计算并加以控制的。而抽样调查则是对一部分单位的统计调查,在实际观察标志值的基础上,去推断总体的综合数量特征。例如,某村种有晚稻3000亩,在稻子成熟后随机抽取50个单位的田块为样本,进行实割实测,求得其平均亩产为410千克,从而推算该村的晚稻总产量为410×3000=1230000(千克)。当然这种推断也存在一定的误差,但与其他统计估算不同,抽样误差的范围可以事先加以计算,并控制这个误差范围,以保证抽样推断的结果达到一定的可靠程度。
抽样调查是必不可少的一种调查方法,但是,抽样调查也有它的弱点。例如,它只能提供说明整个总体情况的统计资料,而不能提供说明各级状况的详细的统计资料,这就难以满足各级领导和管理部门的要求。抽样调查也很难提供各种详细分类的统计资料。因此,抽样调查和全面调查是不能互相代替的。
5.1.1.3 抽样调查的适用范围
抽样调查适用的范围是广泛的,从原则上讲,为取得大量社会经济现象的数量方面的统计资料,在许多场合都可以运用抽样调查方法取得; 在某些特殊场合,甚至还必须应用抽样调查的方法取得。
(1)有些事物在测量或试验时有破坏性,不可能进行全面调查。例如,灯泡耐用时间试验、电视机抗震能力试验、罐头食品的卫生检查、人体白血球数量的化验等,都是有破坏性的,不可能进行全面调查,只能使用抽样调查。
(2)有些总体从理论上讲可以进行全面调查,但实际上办不到。例如,了解某森林区有多少棵树、职工家庭生活状况如何,等等。从理论上讲这是有限总体,可以进行全面调查,但实际上办不到,也不必要。对这类情况的了解一般采取抽样调查方法。
(3)抽样调查方法可以用于工业生产过程中的质量控制。抽样调查不但广泛应用于生产结果的核算和估计,而且有效地应用于对成批或大量连续生产的工业产品生产过程中的质量控制,检查生产过程是否正常,及时提供有关信息,以便采取措施,预防废品的发生。
(4)利用抽样推断的方法,可以对某种总体的假设进行检验,来判断这种假设的真伪,以决定取舍。例如,新教学法的采用、新工艺新技术的改革、新医疗方法的使用等是否收到明显效果,需对未知的或不完全知道的总体做出一些假设,然后利用抽样调查的方法,根据实验材料对所作的假设进行检验,做出判断。
随着抽样理论的发展、抽样技术的进步、抽样方法的完善和统计队伍业务水平的提高,抽样调查方法将在社会经济生活中得到愈加广泛的运用。
5.1.2 几个基本概念
5.1.2.1 总体和个体
总体(population)和个体(item)是统计学中的两个基本概念。对总体和个体有两种理解。一种是具体的理解,即个体是统计问题中的每个研究对象,总体是研究对象的全体。例如在研究某省农民收入统计问题中,每个农户就是个体,该省全体农户组成总体。在这种理解下,总体都是有限的,即包含的个体数有限。另一种是抽象的理解。例如在农民收入统计问题中,我们关心的仅仅是“收入”这个统计指标的数量特征及其分布情况,并不关心其他的指标。“收入”作为一个统计指标可以在一定范围内取数值,就此指标而言不同农户所取的值是不同的,抽取了若干农户就观察到了收入指标这样或那样的数值。而在不同的抽取中观察到的数值又不尽相同,即取值带有随机性。所以这个统计指标是一个随机变量。由于我们关心的仅仅是作为随机变量的统计指标的数量特征及分布,所以我们就把具体的研究对象及其全体放在一边,而把这个统计指标称为总体,其所取的每个可能值称为个体。在这种理解下,总体既可以是有限的,也可以是无限的。当一个总体只取有限个可能值时,则称其为有限总体; 当它可取无穷多个值时,则称其为无限总体。例如在农民收入统计问题中,收入是在一定区间内取数值的,而一个区间包含有无穷多个数,因此从可以取无穷多个值这一点讲,收入总体应理解为一个无限总体。
以上关于总体和个体的两种理解在统计中都有应用。在一个具体的统计问题中究竟应采用第一种理解还是第二种理解,应根据具体统计问题的特点及研究目的而定。一般地说,在抽样调查领域取第一种理解,因为抽样调查中所研究的总体都是非常具体的总体。在经典的统计理论与方法研究中则取第二种理解,后者常可把总体抽象化为一个随机变量进行研究。通常我们以X表示作为总体的随机变量,亦即我们所研究的统计指标。(https://www.xing528.com)
5.1.2.2 样本
为了研究总体X的数量特征和分布规律,必须知道X的信息。如果不收集全面数据,也必须收集其部分数据,利用部分数据提供的有关总体X的信息对X的数量特征和分布规律进行统计推断,这就需要对总体进行抽样观测。为了使统计推断结论具有一定的精确度和可靠度,所需要的信息量不能太少,因而一般我们对总体X不止进行一次抽样观测,而要进行多次抽样观测,比如n次,通过抽样观测就得到总体X的一组观测数据x1,x2,…,xn,其中xi是第i次抽样观测的结果。称( x1,x2,…,xn)为进行一次容量为n的抽样的样本观察值,n称为样本容量。对于一次具体的容量为n的抽样而言,(x1,x2,…,xn) 是完全确定的一组数据; 但是对不同的容量为n的抽样来说,它随每次抽样而改变,即取值带有不确定性。由于我们要依据抽样结果进行分析推断,并研究比较各种推断方法的好坏,因而一般考虑问题时就不应该把一次容量为n的抽样的结果看做固定的n个数据,而应看做n维随机变量( X1,X2,…,Xn),称它为容量为n的样本(sample)。
因此,样本这一概念具有二重性。一般当我们讨论抽样时,样本应理解为n维随机变量( X1,X2,…,Xn); 而在一次具体的抽样中,样本则是n个确定的数据( x1,x2,…,xn),是n维随机变量( X1,X2,…,Xn)的一个观察值。在一个统计问题中样本究竟应作何理解结合上下文不难确定。
我们抽样的目的是对总体X的数量特征和分布规律进行推断,因而要求样本很好地反映总体的特征,这就对抽取样本的方法提出一定要求。通常提出以下两点要求:
第一,代表性,要求样本的每个分量Xi应与总体X有相同的分布。
第二,独立性,要求X1,X2,…,Xn为相互独立的随机变量,即任何一次抽样结果既不影响其他抽样结果,也不受其他抽样结果影响。
满足上述两点要求的样本称为简单随机样本,获得简单随机样本的方法称为简单随机抽样(simple random sampling)。由概率论易知,对有限总体进行无放回随机抽样所得的样本即为简单随机样本。今后若不特别声明,样本均指简单随机样本。
5.1.2.3 统计量
虽然样本提供了总体的信息,但样本提供的信息是分散的,不集中,不便有效地对总体进行推断。为了能有效地推断总体,我们必须对样本进行“加工”,把样本中所包含的有关总体某一特征的信息“提取”“聚集”在一起,这就是根据推断问题的需要构造样本的适当函数,不同的样本函数反映总体的不同特征,一旦有了样本观察值就可以由此给出总体特征的推断值,因此自然要求这种样本函数不包含任何未知参数,称这种样本函数为统计量。
定义5.1 设( X1,X2,…,Xn)是总体X容量为n的样本,若样本函数T =T(X1,X2,…,Xn) 中不含任何未知参数,则称T为一个统计量。
例如,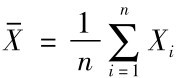 就是一个统计量,称为样本均值;
就是一个统计量,称为样本均值;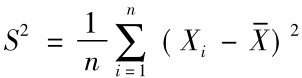 也是统计量,称为样本方差;而
也是统计量,称为样本方差;而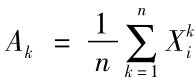 也是统计量,其中k是自然数,称为样本k阶原点矩。
也是统计量,其中k是自然数,称为样本k阶原点矩。
5.1.3 抽样分布
根据样本统计量去估计总体参数,必须知道样本统计量分布。
定义5.2 某个样本统计量的抽样分布,从理论上说就是在重复选取容量为n的样本时,由每一个样本算出的该统计量数值的相对数频数分布或概率分布。
由于现实中我们不可能将所有的样本都抽出来,统计的抽样分布实际上是一种理论分布。
5.1.3.1 样本均值的抽样分布
从单位数为N的总体中抽取样本容量为n的随机样本,在重复抽样的条件下,共有Nn个可能的样本;在不重复抽样条件下,共有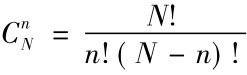 个可能样本。对于每一个样本,我们都可以计算出样本的均值
个可能样本。对于每一个样本,我们都可以计算出样本的均值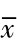 (或s2或p),因此,样本均值是一个随机变量。所有的样本均值形成的分布就是样本均值的抽样分布。
(或s2或p),因此,样本均值是一个随机变量。所有的样本均值形成的分布就是样本均值的抽样分布。
举例说明: 设一个总体含有4个个体,取值分别为:x1=1,x2=2,x3=3,x4=4,则总体分布为均匀分布,且总体均值: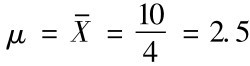 ;总体方差:
;总体方差: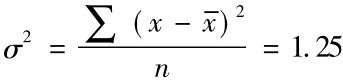 。
。
5.1.3.2 抽样比例的抽样分布
比例即结构相对数,即成数。
总体比例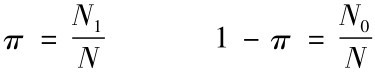
样本比例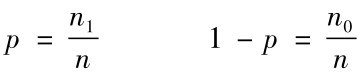
当n很大时,样本比例p的抽样分布可用正态分布近似。
对于样本比例p,若np≥5和n(1-p) ≥5,就可以认为样本容量足够大。
与样本均值分布的方差一样,样本比例的方差对于无限总体,不重复抽样也可按重复抽样来处理;对于有限总体,当N很大,而n/N≤5%,修正系数 会趋于1,不重复抽样也可按重复抽样来处理。
会趋于1,不重复抽样也可按重复抽样来处理。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




