矿产资源密集区的可持续发展警情预测

预测是指对事物或事件未来的情况进行分析和估计，分析和估计的依据是采用科学的理论和方法分析现有所掌握的数据资料。进行预测的目的是采取相应措施以减少事件在将来发生的不确定性，更有利于指引事件未来的发展方向。以社会、经济、环境和生态等子系统的现有数据为依据，建立以这些特征数据为基础的数学模型的过程即是灰色系统理论建模的过程，建立数学模型即可分析各个因素之间的数学逻辑关系，从中可分析出整个系统未来的发展方向和趋势。我国学者邓聚龙先生在1982年一篇论文《灰色控制系统》中首先提出灰色预测的方法。灰色预测以灰色系统理论的动态预测数学模型为基础，经过几十年的发展应用与验证，国内外很多学者专家普遍认为灰色预测是一种比较客观的预测方法，该预测方法在多个学科领域都有着比较广泛的应用。

1.基本原理

灰色预测法是在对现有数据资料分析的基础上，通过建立相应的灰色系统模型，分析出事件的发展规律，是一种对事件未来情况进行科学定量预测的方法。其具体操作步骤如下：

①灰色理论定义了部分信息明确而部分信息不明确的随机变量为灰色量，这些灰色量相应时间内在一定范围内变化的随机过程叫做灰色过程；

②由于灰色量的不确定性，需要运用灰色理论将原有的散乱数据变成比较有逻辑规律可循的数据，根据这些有规律的数据进行数学建模；

③灰色理论还可以通过对建立的灰色数学模型进行修正，以此来提高预测方法的准确度；

④用灰色理论所计算出的预测数据必须经过逆计算过程也叫逆生长过程推算后才能使用。

微分方程描述的动态模型、拉普拉斯变换的线型定常系数模型和时间函数形式的响应模型经常被用于灰色预测方法中数学模型的建立。设描述灰色系统的预测模型GM（n，h）是一个n阶、具有h个变量的数学模型，不同的阶数n和变量个数h所代表的含义都不相同，当阶数n＝1时的模型GM（1，h）称为状态模型，当变量个数h＝1时的模型GM（n，1）称为预测模型，当阶数n＝0时的模型GM（0，h）称为静态模型。状态模型主要依据参考因子数据的预测来完成主因子数据的预测，静态模型只考虑主因素和单个子因素之间的关系，而预测模型的变量个数等于1，阶数为n的n阶导数的数学模型，一般在实际应用当中预测模型的阶数要小于3，因为阶数越高相应的计算量就越大，计算结果的准确度也不高，在实际应用中我们取一阶导数，即预测模型为GM（1，1）。因为模型阶数为1，GM（1，1）模型不能很好地表征系统的动态过程。因此需要计算多次残差来修订GM（1，1）模型，修订过的GM（1，1）模型就能较好地表征灰色系统的行为过程。近年来GM（1，1）模型广泛地应用于生态、经济、社会等领域[190]。

2.GM（1，1）预测模型[191]-[192]

GM（1，1）模型可以对事件在未来特定时间内的变化情况和发展趋势进行估计，这些变化如果是异常情况就可以提前采取补救措施，因此该模型在工业、农业、生态、社会等领域中都有应用意义。

GM（1，1）模型可以削弱原有序列x（0）的不确定性，使模型能够提供更加有用的信息。为了弱化原数据序列的不确定性，需要在建立数学模型之前对原数据进行分析。常用的方法是采用累加的方法，即1-AGO（Accumulating Generation Operator），具体步骤如下[193]：

对GM（1，1）灰微分方程

设有一原始数据序列X（0）：

做一次累加生成（1-AGO）即可得到数列X（1）：

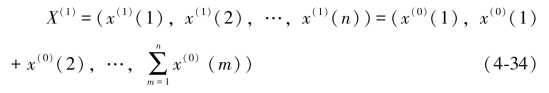
z（1）为x（1）的邻均值等权生成序列，即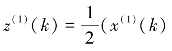于是对X（1）可以建立下述白化形式的微分方程（也称影子方程）为

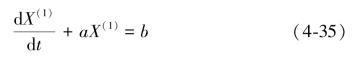
参数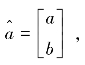其中a称为发展灰数，b称为内生控制灰数，a的有效区间是（-2，2）。应用最小二乘法求解可得

(www.xing528.com)

其中

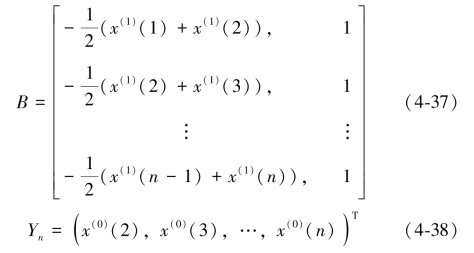
求得方程的解为

对微分方程的解作一次累减生成，即得还原序列

如前所述，GM（1，1）预测模型不能很好地描述系统的动态发展过程，为了提高预测结果的精度和可靠度，需要计算多次残差来修正预测模型，其方法如下：

若按GM（1，1）模型计算值序列还原为灰色系统特征行为数列后，计算其与原始数列x（0）的残差：并分别计算原始数列和残差序列的方差和利用后验差值和小误差概率进行。

GM（1，1）模型精度评价如下：

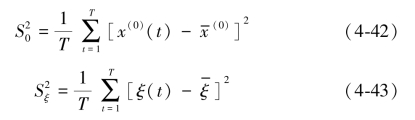
式中，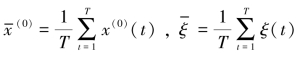

设后验差比值检验系数C和小误差检验值p为

其中，的基本事件/T。

C越小预测结果越好，一般应用中要求C小于0.35。另一个指标是小误差概率要大，所谓小误差是指绝对偏差或者说，相对偏差一般要求p＞0.95，不得小于0.7。

依据检验系数C和检验值p可以评定预测模型的精度。一般地，我们将预测模型GM（1，1）的预测精度分为如表4-4所示等级分类表。

表4-4　预测精度等级分类表

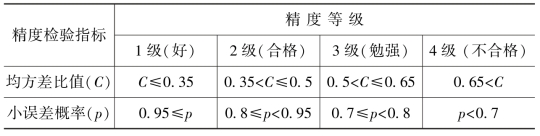
至此，我们完成了灰色系统数学模型的建立以及当模型预测结果精度不符合要求时根据多次计算残差修订预测模型的方法。