【摘要】：对于交易效率的分布，我们参照了Aghion&Howitt的质量梯形模型，假设交易效率的异质性也呈阶梯分布：其中θ＞0衡量了市场整体的交易费用，i越大，ki越小，从而标号越高的交易费用越高。前者的相等与现实不符，我们对于自给自足的产品付出的劳动不同，这是由之前对效用函数的假定引起的，当人的效用函数对不同产品的偏好不同时，算出来的Li的结果自然也会不同，基本上符合对i产品越偏好Li越大的规律。
不妨先假设最后的分工水平为n，即在交易效率正向排序后，决策人在第n个产品上选择了自给自足，第n-1个产品上选择了向外界购买，是否自给自足的临界交易效率在第n个产品的交易效率和第n-1个产品的交易效率之间。对于交易效率的分布，我们参照了Aghion&Howitt（1992）的质量梯形模型，假设交易效率的异质性也呈阶梯分布：
其中θ＞0衡量了市场整体的交易费用，i越大，ki越小，从而标号越高的交易费用越高。
由文定理（Wen，1996）可知，不同时买和卖同种产品，不买和自给同种产品，顶多卖一种产品，对于出卖j产品的人来说：
将（5）（6）（7）代入（1）（2）（3）（4）中可以得到分工水平为n的条件下生产j产品的“消费者—生产者”的决策问题如下：
由（9）代入（8）消去xi，（10）（11）（12）代入（8）消去xj得到最终的间接效用函数：
式（13）的决策问题最优解的一阶条件是：(www.xing528.com)
化简可得：
这说明对于任意的Li，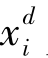
pij都是相等的，后者相等与我们实际相符，相对价格与需求呈反向关系，相对价格的上升会抑制需求。前者的相等与现实不符，我们对于自给自足的产品付出的劳动不同，这是由之前对效用函数的假定引起的，当人的效用函数对不同产品的偏好不同时，算出来的Li的结果自然也会不同，基本上符合对i产品越偏好Li越大的规律。
（14）（15）以及不同产品生产者效用相同时，可得最终效用大小：
U是关于n的函数，当U取到最大值时，此时n的值为最优分工水平。图1为当a=1.8，m=100，θ=1时U关于n的图，U在n=53的时候取到最大。
图1
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
