如何削弱消极互惠行为的影响

在这一部分，我们将证明当程序M成为博弈的备选方案时，参与者的行为将发生改变，并且在某种情况下参与者的消极互惠行为将被弱化。为了证明这一点，构造一个工资设定博弈T3，如图7.3所示。

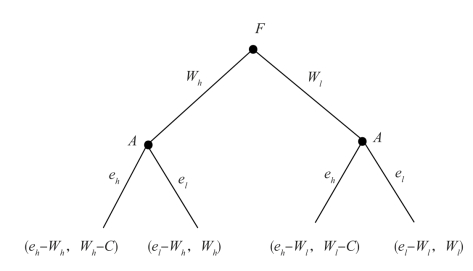
图7.3　博弈T3

其中，参与者F表示雇主，参与者A为其雇用的一个职员A。F首先决定A的工资水平WA，为简化起见，假定工资WA只能取两个值WA∈{WH，WL}，并且WL＜WH。然后，职员A决定他的努力水平ea，同样，假定ea也只能取两个值ea∈{eh，el}，并且el＜eh。

F的利润可以表示为：πF＝ea-WA。另外，假定如果职员A付出高努力的工作水平时，将产生额外的劳动成本C，而付出低努力水平时则无需付出努力成本，于是有职员A的效用水平为πA(WA，eh)＝WA-C，πA(WA，el)＝WA。

最后，为了考虑帕累托改进，假定WH-WL＞C，以保证A付出高努力水平，获得高产生的物质支付大于低工资—低努力产生的物质支付，即πA(WH，eh)＞πA(WL，el)；同时，对于F而言，假定eh-WH＞el-WL，以保证A付出高努力水平，F实现的利润水平大于A付出低努力水平产生的物质支付，πF(WH，eh)＞πF(WH，el)。进一步，假定将高工资与低工资之间的差额限定在2C以内，也就是说C＜WH-WL＜2C。假定A具有互惠偏好，而F则为追求物质利润最大化的理性人。

在博弈T3中，职员A的工资水平是由公司F决定的，因此，公司F直接影响职员A的收入水平，并且受到职员A的互惠偏好的影响。根据Dufwenberg和Kirchsteiger(2004)互惠模型，可以刻画出参与者在博弈T3中的行为特征，具体如下：

结论7.1：在每一个SRE中，当公司F选择WL时，职员A会选择el。

结论7.2：若员工A关于公司F的互惠敏感度为Y，则在每一个SRE中，当公司F选择H时，职员A的选择如下：

(1)当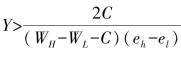时，员工A选择eh；

(2)当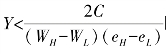时，员工A选择el；

(3)时，员工A以p的概率选择eh，其中

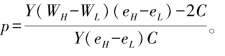
结论7.1证明：不管员工A选择eh或是el，公司F选择WL时A所得到的支付都少于公司F选择WH时A所得到的支付。因此，无论员工A关于公司F策略的信念是什么，F选择WL都意味着F对于A的动机是不善意的。因此，当员工A预期到这一点，会选择el。

结论7.2证明：当公司F选择WH时，员工A能够给予F的最大物质收益为(eh-WH)，最小物质收益为(el-WH)。因此，由式(7.3)可得，对于参与者F来说，公平支付是：

当员工A选择eh时，参与者F的物质支付为(eh-WH)。由式(7.2)得到，员工A选择eh、el时的善意分别为：

为了计算员工A认为公司F选择WH时的善意，需要明确员工A关于公司F对员工A策略的信念的信念(即员工A的二阶信念)，将此表示为p″∈[0，1]，即员工A相信公司F认为自己会以p″的概率选择eh，以1-p″的概率选择el。因此，员工A认为公司F选择WH试图给予自己的物质支付为：

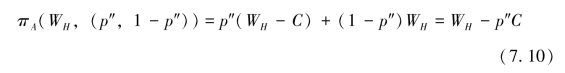
另外，公司F选择WL时，员工A相应获得WL的物质支付。因此，员工A关于公司F选择WH对自己善意程度的推断λiji(bij，Ciji)为：

这样，根据式(7.6)对具有互惠心理的员工A的效用函数的定义，将式(7.8)、式(7.10)、式(7.11)代入式(7.6)，得到当公司F选择WH，且员工A的二阶信念为p″时，员工A选择eh的效用为：

同理，将式(7.8)至式(7.10)代入式(7.6)，得到员工A选择el的效用为：

当UA(eh，WH，(p″，1-p″))＞UA(el，WH，(p″，1-p″))时，员工A会选择eh。于是，由式(7.12)、式(7.13)可得，员工A选择eh的条件是进一步，均衡情况下，员工A的二阶信念是正确的，因此有均衡中p″＝1，于是可得当Y＞时，员工A会选择eh。

反之，当UA(eh，WH，(p″，1-p″))＜UA(el，WH，(p″，1-p″))，即Y(WH-WL-p″C)(eh-el)＜C，员工A会选择el。均衡情况下员工A的二阶信念为p″＝0，于是可得当Y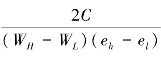＜时，员工A会选择el。

当时，此时员工A在el、eh之间随机选择，此时有于是有均衡情况下，员工A选择eh的实际概率p＝p″，于是可以得到员工选择eh的实际概率为

结论7.2证毕!

现在构造引入了第三方参与者0的博弈T4，如图7.4所示。在博弈T4中，公司F可以自己决定员工A的工资水平W，W∈{WH，WL}。公司F也依据程序M来决定员工A的工资水平。程序M的实质就是引入一个第三方参与者0，由它决定员工A的工资。这里，参与者0可以代表一个虚拟市场，也可以代表一个集体投票程序，甚至可以是“上帝”(比如抛一个硬币)，最重要的是参与者0客观、公正。假定参与者0以q的概率选择员工A的工资水平为WH，以1-q的概率决定员工A的工资水平为WL，且这一概率为博弈参与者的共同知识。

图7.4　博弈T4

从直觉上来看，博弈T4意味着参与者1具有两个不同的决策程序，即公司F可以通过自己决定工资水平，也可以通过程序M，让参与者0在WH与WL之间做出选择。由于参与者0独特的地位与性质，决定了参与者0引导的子博弈最终赋予每一个参与者的期望物质支付成为新的公平支付，这一公平支付不随人们信念的更新而改变，只与参与者0的行为策略ω有关。(www.xing528.com)

以上的假设说明，当公司F选择程序M，将工资水平的决定权交给参与者0时，公司F对待员工A的善意为0，员工A感知到的公司F的善意也为0，因此，可以将由公司F引导的子博弈过程看成一个标准博弈过程，其中每一个参与者的心理支付为0，也就是说此时，每一个参与者只追求物质支付，其行为特征与理性条件下的子博弈完美均衡策略一致。

通过简单的分析可以看到，在参与者0引导的子博弈中，员工A的均衡策略为(el，el)，由此可得，员工A的公平支付为πelA(w)＝qWH＋(1-q)×WL，而公司F的公平支付为，并且只与ω有关。

给定以上说明，关于博弈T4可以得出以下结论：

结论7.3：在每一个SRE中，当公司F选择WL时，职员A选择el。

结论7.4：在每一个SRE中，当公司F选择WH时，职员A的选择如下：

①当＜q＜1时，员工A的策略是：

若，则员工A选择el；

若，则员工A以p的概率选择eh，

其中，并且此时0＜p＜1-

②当时，员工A的策略是：

若，则员工A选择el；

若则员工A选择eh；

若时，员工A以p的概率选择eh，其中p＝，并且此时＜p＜1。

结论7.3证明：在博弈T4中，假定当公司F选择WL时，员工A相信公司F认为自己选择eh的概率为p″。给定这一假定，可知员工A选择el的效用为：

员工选择eh的效用为：

由式(7.14)、式(7.15)可得，员工选择el的效用水平必然大于其选择eh的效用水平，因此当公司F选择WL时，员工的均衡策略是el。

结论7.3证毕!

结论7.4证明：在博弈T4中，假定当公司F选择WH时，员工A相信公司F认为自己选择eh的概率为p″。给定这一假定，可知员工A选择el的效用为：

员工选择el的效用水平为：

当(7.18)式小于零，即Y(eh-el)((1-q)(WH-WL)-Cp″)＜C时，员工A会选择el。由于q＜1，且p″＝0，因此有员工选择el的条件是此时员工A选择均衡策略el与q无关。

当式(7.18)大于零时，即Y(eh-el)((1-q)(WH-WL)-Cp″)＞C时，需要分两种情况进行讨论。

情况一：若(1-q)(WH-WL)＞C，员工A会选择eh(此时p″＝1)，因此员工选择eh的条件是Y(eh-el)((1-q)(WH-WL)-C)＞C。因此，若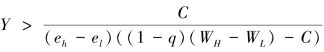，且q＜1-，员工A会选择eh。

情况二：若(1-q)(WH-WL)＜C，即q＞1-时，即使，员工A的均衡策略也不是eh。此时员工A的均衡策略是一个随机化的策略，且Y(eh-el)((1-q)(WH-WL)-Cp″)＝C成立，又由于均衡情况下员工A的二阶信念是正确的，即p＝p″，因此得到而且由于q＞1-，可知p＜1-。

当且q＜1-时，eh、el均不是员工A的均衡策略。此时员工A具有一个随机化的均衡策略，且Y(eh-el)((1-q)(WH-WL)-Cp″)＝C必然成立，将p＝p″代入，得到由于q＜1-，故有1-＜p。

对比博弈T3、博弈T4，不难发现当公司F选择WL时，员工A均会选择el，但当公司F选择WH时，员工A的行为存在差异。当1-时，相对于博弈T3，员工A在博弈T4中更倾向于选择el，当时，由于C＜WH-WL＜2C，可得q＜，进一步得到＜1，因此有：

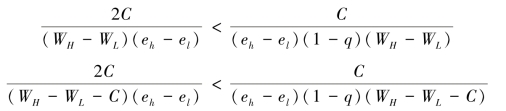
且当q足够小时，成立，进而可推知，当q足够小时，即时，相对于博弈T3而言，博弈T4中员工A的行为更倾向于选择eh。因此，当博弈T4中植入公平的第三方参与者0时，由于参与者0的介入产生了一个新的公平支付基准，员工A的正互惠效应与负互惠效应可能会有不同程度的强化与削弱。比如，在博弈T4中，给定公司F选择WH，则当q足够大时 员工A的消极互惠行为得到强化，而积极互惠行为被削弱；当q足够小时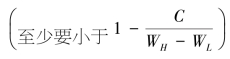，员工A的积极互惠行为得到强化，而消极互惠行为被弱化。

综合上述分析，结论7.4证毕!