模型求解与分析技巧

(1)比较基准：代理人纯粹自利情形下的最优报酬合约。

作为比较基准，首先考虑代理人纯粹自利情形下(α＝0)的最优激励合约。对于纯粹自利的代理人，其确定性等价收入为CEi＝k＋mai＋求一阶条件，得激励相容约束为＝m(上标S表示代理人纯粹自利的情形)。相应地，委托人的最优化问题可简化为：

运用一阶方法解上述规划，可得：

式(5.33)、式(5.34)给出了代理人自利情形下的最优激励合约。其中，式(5.34)表明，当代理人之间的业绩正相关(r＞0)时，应当将代理人j(j≠i)的业绩以负权重写进代理人i(i＝1，2)的报酬合约。

事实上，根据标准代理理论的充足统计量原则(sufficient statistics，Holmstrom，1979)，由于代理人j的工作业绩yj能够提供关于代理人i(i＝1，2)行为的有价值的额外信息，因此给予代理人i的补偿不仅应该基于绝对业绩yi，还应该考虑到相对业绩yj，这样可部分消除代理人受到共同冲击的影响，更精确地推断代理人的努力程度，从而更有效地激励代理人。这正是相对业绩评价的基本含义。此外，从式(5.33)可以看出，代理人的风险厌恶程度ρ越大、收入越不稳定(σ2越大)、代理人之间业绩相关程度r越小，则最优激励强度mS越小。因此，给定nS，最优mS是关于风险与激励之间权衡的结果。

(2)代理人具有公平偏好情形下的最优报酬合约。

①公平偏好对报酬合约的影响。

(a)公平偏好的激励效应。

对式(5.27)求最优化一阶条件，得到：

由式(5.25)可得：

均衡状态下，于是有Δ＝0，则式(5.36)简化为：

将式(5.37)代入式(5.35)，可得：

于是，有：

由式(5.39)可以看出，若β≠1，则给定合约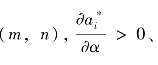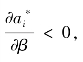表明代理人对劣势不平等的厌恶会提高努力水平，优势不平等厌恶心理则会降低努力水平，但整体而言不平等厌恶心理会激励代理人付出更高的努力水平，即，从而产生有利于委托人的激励效应。特别地，当β＝1，即代理人对于劣势不平等和对优势不平等的厌恶程度相同时，不平等厌恶心理不会对代理人的努力水平产生任何影响，即

(b)公平偏好的参与约束效应。

对于具有不平等厌恶心理的代理人而言，因报酬的不平等会遭受不平等负效用，进而参与约束式(5.28)要求委托人对代理人提供额外的不平等负效用补偿，即不平等贴水(inequity premium)。这是不平等厌恶的参与约束效应。由于均衡情况下Δ＝0，因此当m＞n时，由式(5.25)可得代理人i(i＝1，2)所遭受的均衡期望不平等负效用为：

式(5.40)表明，给定报酬合约(m，n)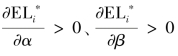，，说明代理人的公平偏好越强，其所遭受的期望公平负效用越大，则委托人给予代理人的不平等贴水越多。

②最优激励合约。

(a)α＝β情形下的最优合约。

在代理人有对称程度的不平等厌恶心理，即β＝1的情形下，不平等厌恶仅通过参与约束效应影响最优激励合约的设计，激励效应不起作用。根据式(5.39)、式(5.40)，当β＝1时委托人的最优化问题可简化为：

将式(5.41)代入式(5.42)，并分别对m、n求一阶偏导，得到最优化一阶条件为：

由式(5.44)得：(https://www.xing528.com)

注意到n≤m，因此进一步可得：

当n＜m时，将式(5.45)代入式(5.43)，可解得：

当n＝m时，(5.41)式简化为，求一阶条件，得到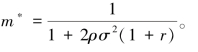综合n＜m和n＝m两种情况，则代理人的最优产出分享系数由下式给出：

相应地，代理人报酬与另一代理人业绩的最优相关系数n*为：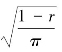

式(5.48)、式(5.49)表示，当n＜m时，最优m*、n*取各自表达式中左边数值；当n＝m时，最优m*、n*则取各自表达式中右边数值。

通过比较式(5.34)和式(5.46)可知，如果代理人对优势不平等和劣势不平等的厌恶程度对称，即α＝β时，n*是在风险与不平等之间综合权衡的结果：一方面，由于代理人的产出正相关，因此可以将相对业绩yj以负的权重-mr写进代理人i的报酬合约中，以剔除更多外部不确定因素的影响；另一方面，当α＝β时，公平偏好仅通过参与约束效应影响激励合约，而为了减少对代理人的不平等贴水(m-n)(α＋β)σ，委托人应该选择n＞0的团队业绩合约。因此，n*是在选择RPE以降低风险成本，与选择TPE以降低不平等贴水之间权衡的结果。因此，可以得到结论5.3。

结论5.3：如果代理人对优势不平等和劣势不平等的厌恶程度相同，则其报酬与另一代理人业绩的相关系数n*是在选择RPE以降低风险成本，与选择TPE以降低不平等贴水进行权衡的结果。

同时，通过对式(5.34)、式(5.46)的比较可以发现，代理人存在不平等厌恶心理时，其报酬与另一代理人业绩的最优相关程度n*较代理人自利时的相关程度nS大，且代理人对公平的偏好α越强，n*越偏离于nS。当α足够大时，n*必然为正值，这意味着即使代理人之间业绩正相关，委托人也应该选择TPE而不RPE。为此，可以得到推论5.3：

推论5.3：如果代理人公平偏好倾向足够强，那么委托人应当对代理人实行TPE，而不是RPE。

不同于标准代理理论的结论，结论5.3和推论5.3表明，当代理人存在公平偏好时，RPE不再是降低代理人业绩报酬风险、进而改善其努力水平的最优策略，而应采用团队业绩评价的策略来缩小代理人之间收入差距，即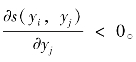该结论从行为经济学的视角为揭开“RPE之谜”提供了新的理论解释。当企业在设计管理层的薪酬合约时，引入RPE尽管会降低风险成本，但同时可能造成额外的不平等贴水，是否采用RPE应该取决于这两方面的权衡。如果管理层具有强烈的追求公平的心理，那么对于企业而言，团队业绩评价是比相对业绩评价更优的薪酬制度安排。

推论5.4：对于具有公平偏好的代理人，委托人对其激励强度m*不会高于对于自利代理人的激励强度mS。

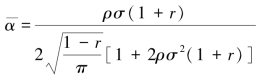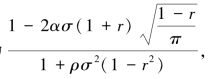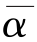证明：当α＝β时，由式(5.48)可知，代理人的公平偏好强度存在一个临界值，使得当0≤α＜α时，最优激励强度m*取值为而当α≥时，m*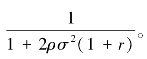＝进一步，当0≤α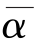＜时，m*是α的严格减函数，即公平偏好强度越大，则对代理人的激励强度越小；且α＝0时，m*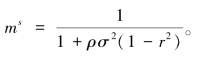＝因此，当0≤α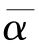＜时，m*≤ms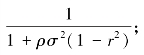＝当α≥α时，同样有综合上述分析，可得引理推论5.4的结论。

证毕!

标准代理理论认为，对于管理者的激励，最好办法是将其报酬与经营业绩挂钩，即通过在高水平业绩时付给高水平报酬，可以激励努力工作。因此，需要提供较高强度的激励。然而，以实证研究为主的文献，如Jensen和Murphy(1990)[134]、Tosi等(2000)[160]等并不支持代理理论的这一论断，而是发现业绩报酬之间存在低敏感性。对于传统代理理论无法解释的业绩报酬低敏感性困惑，Englmaier和Wambach(2010)[94]、魏光兴和覃燕红(2010)[161]、黄健柏(2009)[162]等都从行为经济学的视角，通过将公平偏好引入单代理模型，证明如果考虑代理人的公平心理，那么业绩报酬相关系数不应该如标准代理理论所预测的那么高。本节推论5.4同样表明，如果考虑到公平偏好的存在，那么公平偏好会降低管理者报酬的业绩敏感性。

(b)α≠β情形下的最优激励合约。

当α≠β时，激励相容约束由式(5.39)给出。令，则委托人的最优化问题可描述为：

将式(5.51)代入式(5.50)，并分别对m、n求一阶偏导，有：

令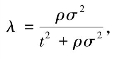由式(5.53)可得：

(5.54)式表明，代理人之间最优的报酬业绩相关系数n取决于以下三个因素：首先，根据标准代理理论的充足统计量原则，应当将相对业绩以负的权重写入代理人的薪酬合约中，即n取负值(表达式第一项)；其次，由于公平偏好的参与约束效应的影响，从减少不平等贴水的角度，委托人对代理人应当采用团队业绩评价，即n应当取正值(表达式第二项)；最后，如果考虑公平偏好的激励效应，那么从激励代理人的角度，n应该取负值(表达式第三项)。因此，代理人之间报酬业绩相关系数n是在风险、激励与不平等三者之间权衡的结果。

结论5.4：如果代理人对优势不平等和劣势不平等的厌恶程度不对称，那么最优薪酬合约是在选择RPE降低风险分担并提供激励，与TPE以降低不平等贴水之间权衡的结果。