构建公平偏好的委托代理模型并求解

(1)模型的基本假设。

假设1：在劳动力市场只存在一个雇主(委托人)和一个雇员(代理人)，委托人雇用代理人从事某项工作，委托人是风险中性的经济人，以获得最大收益为目标；代理人是风险规避的且有公平偏好的，他不仅关注个人利益，而且在乎自己的利益与委托人之间公平收入分配的程度，其效用函数为μ＝e-ρw，ρ表示风险规避度量(λ＞0)，w为实际货币收入。

假设2：a代表代理人的努力程度，而代理人的产出函数为π＝a＋θ，θ为代理人面临的随机因素的影响，服从分布N(0，σ2)；代理人努力的成本函数b＞0为努力的成本系数，表示代理人越努力，则所付出的成本越大，且随着a增大，代理人努力的成本增加更快。

假设3：代理人获得的报酬W(π)是关于产出π的线性函数，W(π)＝m＋nπ，其中，m表示代理人不受产出影响的固定收入，n是代理人的产出分享系数。

假设4：代理人具有公平偏好，FS模型将行为人的公平偏好刻画为不平等厌恶，即人不仅关心自己的物质收益，还关心与其他人比较物质收益分配是否公平。因此，借鉴FS模型对公平偏好的刻画，代理人的实际收入为：

其中α表示代理人对处于劣势不平等，即其劳动报酬低于委托人剩余的厌恶程度，β表示代理人对优势不平等，即其劳动报酬高于委托人剩余的厌恶程度。根据博弈实验结果，不妨假设α∈[0，1]，β∈，特别地，当α＝β＝0，代理人具有纯粹自利偏好。

假设5：代理人保留收入为0。

对于风险中性的委托人，其期望效用等于其期望收入，即

根据假设4，当代理人获得的劳动报酬小于委托人的剩余即W(π)＜π-W(π)时，代理人的实际收入水平为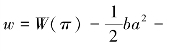，整理后得其中τ＝n-α＋2nα，于是代理人的确定性等价收入为：

当代理人获得的劳动报酬高于委托人的剩余即π-W(π)＞W(π)时，代理人的实际收入水平为，其中ξ＝n＋β-2nβ，于是代理人的确定性等价收入为：

分别表示代理人获得劳动报酬低于委托人剩余及劳动报酬高于委托人剩余两种情形下的风险成本。

(2)代理人厌恶劣势不平等的模型分析。

当代理人的收益小于委托人即W(π)＜π-W(π)，委托人的激励问题可以表述为规划问题[P1]：

其中，式(4.13)、式(4.14)分别为代理人的参与约束(IR)和激励相容约束(IC)。

①信息对称下的模型求解。

当委托人能够观测到代理人的努力水平时，代理人的努力水平a是对称信息，此时代理人的激励相容约束式(4.14)不起作用，任何水平的a都可以通过满足参与约束的强制合同来实现。易知，式(4.13)是束紧的，于是有：

将式(4.15)代入式(4.12)，可以求得代理人在对称信息下的最优努力水平为：

其中上标S表示对称信息，下标da则表示代理人是厌恶劣势不平等的。进一步可得对称信息下代理人的产出分享系数、固定工资水平以及委托人的均衡期望收益分别为：

式(4.18)、式(4.19)所给出的结果表明，当代理人厌恶劣势不平等时，对称信息下，委托人会分配给代理人一半的收益分享，以避免后者因劣势不平等遭受效用损失。特别地，注意到在代理人具有纯粹自利偏好，即α＝β＝0情形下，若信息是对称的，则均衡解为：

式(4.20)至式(4.22)所给出的均衡结果与HM模型在对称信息下的均衡结果是完全一致的。

②非信息对称下的模型求解。

非对称信息条件下，委托人不能观察到代理人的努力程度，激励相容约束(IC)此时发挥作用。对式(4.14)求一阶条件，得到：

将式(4.15)、式(4.23)代入目标函数中求解，得到最优化一阶条件为：

上标AS表示信息不对称。进一步可得代理人的固定工资水平、委托人的期望收益分别为：

特别地，在代理人具有纯粹自利偏好，即α＝β＝0时的均衡解为：

③模型结果分析。(www.xing528.com)

结论4.5：无论委托人与代理人之间的信息是否对称，在代理人劣势不平等厌恶心理的影响下，代理人都获得收益分享，且最优收益分享比例与代理人公平偏好程度正相关。

根据经典委托代理理论，在信息对称的情形下委托人只需支付给代理人固定工资。但是，当考虑代理人的公平偏好心理时，即使信息是对称的，为了降低代理人因对劣势不平等的厌恶所遭受的期望效用损失，委托人会给予代理人一定比例的产出分享。当委托人与代理人之间存在信息不对称时，比较式(4.25)和式(4.29)可以发现，委托人给具有公平偏好的代理人的收益分享较完全自利代理人的收益分享高，且，其中正是因考虑到代理人的公平偏好，委托人会给予其的额外激励。进一步，由式(4.17)、式(4.25)可得，，表明无论信息是否对称，代理人最优分享比率都会与其公平偏好程度正相关。

结论4.6：无论委托人与代理人之间的信息是否对称，代理人都会提高其努力程度来回报委托人。

由上述分析可知，当委托人与代理人之间信息对称时，；而当委托人与代理人之间存在信息不对称时，。因此，当代理人厌恶劣势不平等时，其努力水平高于完全自利的代理人。这是因为，委托人在知道代理人具有劣势不平等厌恶心理的情形下会给予代理人更多的收益分享，而代理人也会通过增加自己的努力程度来回报委托人。进一步，由(4.18)式、(4.28)式可得，，这意味着代理人的劣势不平等心理越强，其努力水平会越高。

结论4.7：基于代理人公平偏好心理的新的报酬契约实现了帕累托改进。

传统代理模型中，最优报酬契约的参与约束条件要求代理人获得的期望支付等于其保留收入水平。但是，在考虑代理人劣势不平等厌恶心理的情形下，最优报酬契约要求委托人必须对代理人因不平等厌恶心理遭受的期望效用损失给予补偿，而获得公平收入的代理人会提高自己努力水平来弥补委托人牺牲的利益，在这种情况下委托人的利润比代理人选择传统代理模型中最优努力程度时获得的利润高：分别由式(4.19)、式(4.22)以及式(4.27)、式(4.30)可得，

因此，基于代理人劣势不平等厌恶心理的报酬契约，在不减少代理人收入的同时，为委托人带来比HM模型更高的收入，因而实现了帕累托改进。

结论4.8：在不对称信息的情况下，最优报酬契约是寻求激励、保险与公平三者之间的平衡。

由式(4.25)可得，表明是关于代理人劣势不平等厌恶心理α的递增函数，这意味着代理人对公平的关注程度越高则其要求分享的利润越大。同时，，即代理人越是风险规避、产出的方差越大，代理人越是害怕努力工作，代理人的最优风险分担越小。因此，最优报酬契约是激励、公平与保险的权衡。

(3)代理人厌恶优势不平等心理的模型分析。

当委托人的收益低于代理人的收益时，W(π)＞π-W(π)，代理人将产生优势平等厌恶心理。在此情况下，最优化激励问题可以表述为规划问题[P2]：

①信息对称下的模型求解。

信息对称条件下，易得均衡解为：

进一步可得委托人的期望收益为：

下标a表示代理人厌恶优势不平等的情形。

②非信息对称下的模型求解。

在信息不对称时，式(4.33)等价于：

参与约束式(4.33)束紧，于是有：

将式(4.38)、式(4.39)代入目标函数式(4.31)求一阶条件，得到：

模型的最优化一阶条件为：

委托人的均衡期望收益为：

③模型结果分析。

结论4.9：在信息对称和不对称的情况下，代理人的优势不平等厌恶心理会降低自己的努力程度，并且会改变报酬契约的结构。

通过分别比较式(4.20)和式(4.34)、式(4.28)和式(4.40)，可以发现优势不平等厌恶对代理人的最优努力水平会产生负面影响：代理人在信息对称时的努力程度、信息不对称时的努力程度，分别低于代理人纯粹自利的努力程度，即。这表明，当代理人的收益低于大于委托人，代理人会通过降低努力程度、减少利润的方式缩小与委托人之间的收益差距。事实上，由式(4.34)、式(4.40)可得，代理人越厌恶优势不平等，则努力水平越低，即、

进一步，由式(4.35)可以发现，当代理人具有优势不平等厌恶心理时，其在信息对称情形下最优产出分享系数nS a＜0，表明此时代理人由于厌恶自己收入高于委托人，会自愿将自己收入中的一部分返还给委托人，以减少两者之间的收益差距。由式(4.41)可得，在信息不对称的情况下，只有当代理人的优势不平等厌恶程度达到一定程度，即时，＜0，才会出现代理人自愿返还收入的情况；当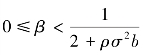时，＞0，委托人因信息不对称而给予代理人的激励大于代理人因优势不平等心理而返还的利润，代理人仍会分享利润；当时，＝0，代理人只获得固定工资，而不分享利润。