互惠偏好对劳动关系的激励效应分析

本部分内容在Dufwenberg和Kirchsteiger(2004)[82]研究的基础上，利用序贯互惠均衡理论，设定两个工资博弈模型，当工人受到互惠动机的影响时，高的工资奖励会促使员工更加努力地工作，而低工资则会使得员工维持于工资相等的努力水平甚至更低的努力水平，而企业最终也会选择高的报酬水平，促使员工更加努力地工作，从而提高企业的利润。

(1)DK模型[82]。

下面首先对Dufwenberg和Kirchsteiger(2004)提出的互惠效用函数(简称为DK模型)进行简单描述。由于只考虑双人博弈的情形，因此假设参与者的集合N＝{1，2}。用Ai表示参与人i(i∈N)的策略集，Bij为参与者i关于参与者j策略的信念集，Bij＝Aj，i，j∈N；Ciji为参与者i关于参与者j关于参与者i策略的信念的信念集。于是，bij∈Bij表示参与者i关于参与者j策略的信念(一阶信念)，而ciji∈Ciji表示参与者i所认为的参与者j关于参与者i策略的信念的信念(二阶信念)。进一步，参与人i的支付可定义为：

(4.1)式中πi(ai，bij)代表参与者i得到的可测量的客观的“物质回报”(如薪酬)。

则表示参与者i的“互惠回报”：Yi＞0参与者i的互惠敏感度，Yi的值越大，说明参与者i对互惠的敏感度越强；κij(ai，bij)表示参与者i对参与者j的善意程度，κij(ai，bij)＞0表示参与人i对参与人j是友善的，κij(ai，bij)＜0则意味着i对对方是不善的；λiji(bij，ciji)表示的是参与人i对于参与者j对自己善意程度的推断，即二阶信念：如果参与者i推断参与人j对自己是友善的，则λiji＜0，如果参与者i推断参与人j对自己是不友善的，则λiji＜0。按照互惠的定义，当κij＞0时，λiji＞0，即若参与人i认为对方对自己是友善的，则自己也会善意对待对方，反之亦然。

参与人i对参与人j的善意程度κij(ai，bij)可进一步描述为：

其中：

这里是参与人j关于参与人i的公平支付，被定义为给定参与人j的策略bij，参与人i的策略ai给参与人j带来的最大收益与最小收益的平均值。于是，参与人i对参与人j的善意程度κij(ai，bij)就被描述为参与人i的策略为参与人j带来的收益与参与人i可以给参与人j带来的平均收益的差值。

类似地，将参与人i对于参与人j对自己善意程度的推断λiji(bij，ciji)定义为：

这里是参与人i关于参与人j的公平支付，被描述为：给定参与人i对于参与人所认为的参与者j关于参与者i策略的信念，参与人i所认为的参与人j的策略bij给参与人i带来的最大收益与最小收益的平均值，这样λiji(bij，ciji)就可理解为信念即参与者i感知到的参与者j的策略给参与者i带来的收益与参与者j能够给参与者i带来的平均收益的差值。

(2)互惠偏好对劳动关系的微观(激励)效应分析。

下面将利用DK模型所定义的互惠偏好效用函数，建立两个考虑员工互惠性偏好的工资设定博弈模型，对互惠偏好的激励效应进行分析。

首先，我们不考虑雇主(F)的效用函数，构造一个基础博弈G0来初步分析互惠对于均衡的影响。假设雇主选择以工资水平w(w＞0)雇用应聘者(A)或者不雇用A；若A被雇用，则他在工作中可以选择高努力水平或低努力水平，若选择高努力水平时，则需付出努力成本c，c＞w，相应地A的支付为w-c，若选择低努力水平，则努力成本为0，相应地A的支付为w。图4.1给出了描述该博弈的一个简化的博弈树G0(该博弈树中只给出了应聘者A的支付)。

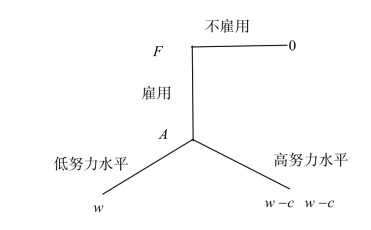
图4.1　博弈G0

如果F选择雇用A，那么F是否对A善意，这取决于F的信念。若F相信A会以100%的概率选择低努力水平，那么F雇用A为后者带来的收益就是w，相比之下若F作出不雇用的决策则为A带来的支付则是0，根据式(4.2)、式(4.3)，有，这表明F对A是善意的。同理，如果F相信A会选择高努力水平并因此选择雇用A，那么，因此F对A是不善意的。

均衡情况下，A能够正确推断F对自己的善意程度，即λAFA＝κFA。因此，如果A具有互惠偏好，则他如何反应将取决于λAFA的正负。同时，均衡情况下，F也能够正确推断A对自己的善意程度。为了进一步求解该博弈的序贯互惠均衡，还需要进一步对F和A对互惠的敏感度和F的效用函数进行假设。为此，我们进一步考虑两种情形下的工资设定博弈：一种情形是当A面临其他工人竞争该职位时A与F之间的博弈，另一种情形则是F面临外部劳动力市场上竞争者时与A之间的博弈。

博弈1：假设两个同质工人竞争某公司发布的一个职位。F决定雇用谁，被雇用者决定自己的努力水平。该博弈包括三个阶段：

阶段1：两个参与者同时提出工资请求w，为简化问题分析假设w只能取两个值，即w∈{wL，wH}且wL＜wH。

阶段2：公司F接受其中一个请求，记作wA，假设F雇用了工人A。

阶段3：A对F的雇用价值由其在工作中的努力水平eA决定，eA∈{eL，eH}，即A可以选择表示努力工作的高努力水平eH，也可以选择表示偷懒的低努力水平eL，eL＜eH，A选择低努力水平和高努力水平的成本分别为cL和cH，cL＜cH。

F的利润为：πF(wA，eA)＝eA-wA，如果不考虑A的互惠偏好则其物质收益为πA(wA，eA)＝wA-cA。为了保证问题分析是有意义的，假设对社会而言被雇用者选择高努力水平更有价值，即eH-eL＞cH-cL。

假设A若被拒绝则其物质收益为0，同时A接受低工资并付出低努力水平所获得的物质收益也为0，即πA(wL，eL)＝wL-cL＝0(假设被拒绝的申请者总是能够在其他某个地方找到一个低工资-低付出的工作)。进一步，对于A而言，接受低工资水平并付出高努力水平比其外部机会更糟糕，即：

πA(wL，eH)＝wL-cH＜0。

为了允许帕累托改进，假设工资水平满足：高工资—高努力水平的组合较低工资—低努力水平的组合，能够给A带来更多的物质收益，并给F带来更多利润，即πA(wH，eH)＞πA(wL，eL)，πF(wH，eH)＞πF(wL，eL)。因此，低工资—低努力水平的组合既不符合A的利益，也不符合F的利益。

另外，假设A的互惠敏感度为YA。(www.xing528.com)

根据上述假设，可以用如图4.2所示的博弈树来描述博弈G1。

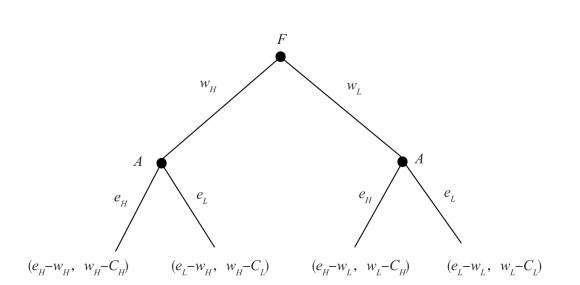
图4.2　博弈G1

通过分析容易发现，如果不考虑A存在的互惠偏好，则无论A接受什么样的工资水平，他都会选择低努力水平；F预期到这一点，也会选择接受低工资请求。因此，在不考虑A互惠偏好的情形下，子博弈精炼纳什均衡的结果是(wL，eL)。但是，如果考虑A的互惠偏好，结论可能会发生改变。

结论4.1：当员工存在互惠偏好时，在每个序贯互惠平衡中有：

(a)如果F接受了低工资请求，那么A会选择低努力水平。

(b)如果F接受高工资请求，那么当A的互惠敏感度足够强，即Y＞2(cH-cL)/[(wH-wL)(eH-eL)]，他会选择高努力水平。

证明：首先考虑F接受低工资请求的情形，我们可以通过反证法证明结论4.1(a)是成立的，假定F接受了低工资请求，而A作出高努力水平的响应，此时A的物质收益为πA(wL，eH)＝wL-cH。均衡情况下F的信念是正确的，因此F能够正确预期A的高努力水平。根据假设有πA(wL，eH)＜0，这意味着A的物质收益低于其保留效用，F知道这一点因而这表明F对A是不善意的，因此kFA＜0。均衡情况下A能够正确推断F对自己的善意程度，因此λAFA＜0。根据前述对参与人支付的定义式(4.1)，可以看出A会必然会对F的不善意行为作出不善意的回应，即选择使κAF＜0的行动，因此A会选择低努力水平，这与前面的假定矛盾。因此，结论4.1(a)成立。

接下来考虑F接受高工资请求的情形。当A具有互惠偏好时，根据DK模型可知，当F选择接受高工资请求时，若A选择高努力水平，对F的善意程度为若A选择低努力水平，则其对F的善意程度为κAF＝eL-wH-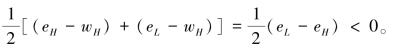

进一步，假定当A可以自由选择努力水平时，其选择高努力水平的二阶信念为π，即A相信F认为自己选择高努力水平的概率为π；那么，A认为F给予其的最大期望支付为：π(wH-cH)＋(1-π)(wHcL)，最小支付为(wL-cH)。根据式(4.4)、式(4.5)可知，当F选择接受高工资请求时，A所感知到的善意为：

λAFA＞0，表明当F接受高工资请求时，A感知到F对自己是善意的。根据式(4.1)，可得当F接受高工资请求时，A选择高努力水平的效用为：

A选择低努力水平的效用为：

当式(4.7)大于式(4.8)时，A选择高努力水平，此时π＝1，代入得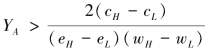。也就是说，当时，若F接受高工资需求，A也会选择高努力水平。结论4.1(b)成立。进一步，由于πF(wH，eH)＞πF(wL，eH)，因此当Y＞时，F也会接受高工资请求。这样，可以得到结论4.2。

结论4.2：如果，则在每个序贯互惠平衡中，公司都会接受高工资请求。

博弈2：假设一个公司内部员工(简称“局内人”)已经被以高工资wH雇用，一个外部劳动力市场上的竞争者(简称“局外人”)则试图得到“局内人”的这份工作，为此可以构建一个三阶段完全信息动态博弈模型。

阶段1：“局外人”要求工资w0，w0∈(wL，wH)。

阶段2：F接受或者拒绝这个请求。如果接受，“局外人”就以工资w0获得雇用，“局内人”将被解雇并不得不接受外部选择，从而获得其保留效用水平0；如果公司拒绝“局外人”的请求，“局内人”将继续以工资wH被雇用，“局外人”仍未被雇用，其效用水平为0；同时，若公司雇用了“局外人”，则将承担一个微量的招聘成本T，0＜T＜wH-wL。

阶段3：被雇用的工人A选择高努力水平或低努力水平eO∈(eL，eH)。

容易看出，如果不考虑个人的互惠偏好，则子博弈精练纳什均衡结果就是(wH，eL)。然而，如果“局内人”和“局外人”都受互惠动机的激励，结果将会发生改变。

结论4.3：每个序贯互惠平衡满足：

(1)如果F接受低工资要求，那么若“局外人”被雇用，他将会选择低努力水平。

(2)如果F接受高工资请求，则当“局外人”的互惠动机足够强，即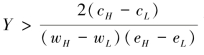时，“局外人”若被雇用则会选择高努力水平。

(3)如果F拒绝了“局外人”的工资请求，则当被雇用的“局内人”的互惠动机足够强，即时，“局内人”会选择高努力水平。

证明：根据结论4.1，在考虑员工互惠偏好的情形下，如果F接受了“局外人”的低工资的请求，那么他将会选择低努力水平“交换”F的低工资水平；同时，无论F接受“局外人”的高工资请求，还是拒绝“局外人”的高工资请求而选择继续雇用“局内人”，只有当员工互惠动机满足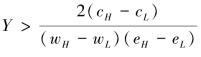时，“局外人”会以高努力水平“回报”F的高工资水平。但是，考虑到雇用成本T的存在，因此F以高工资水平雇用“局外人”是一个次优选择。接受“局外人”的低工资请求也不是最优的，因为这会导致低努力水平。因此，即使“局外人”提出削减工资，也无法获得雇用。于是，可以得到结论4.4。

结论4.4：如果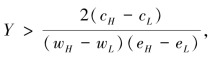那么存在一个“F不雇用‘局外人’”的连续性互惠均衡。

效率工资理论(Akerolf，1982)认为，企业付给员工的高于市场出清水平的工资，能够有效调动员工积极性，提高生产率与企业经营绩效。该理论的基本假定之一是：人类有着“投桃报李”的天性，因而企业向员工支付效率工资是用来交换其加倍工作的，而员工的加倍工作也是用来获取企业的高工资。因此，这种互惠原则正是效率工资起作用的基本条件。

本节这部分建立了两个考虑员工互惠偏好的工资设定模型，进一步揭示出在员工互惠动机足够强的条件下，高工资可诱发员工投桃报李而提高生产力，低工资则会引发员工“不满”从而降低努力水平，因此即使劳动力市场有超额供给，企业也不会选择降低工资，雇佣关系也会趋于稳定。