任务优先规则分类与常见规则

对于串行或并行进度生成机制的分析说明，优先规则在上述启发式算法中起到了很关键的作用。因此有必要对各类优先规则进行详细的分析。

在进度生成机制中，优先规则（priority rule）用于从候选任务集合Dg中选择一项任务。优先规则对集合Dg中的每个任务j都赋予一个优先值v（j），并根据规则从集合Dg中选择优先值最大或最小的任务。如果多个任务存在相同的优先值，则需要找到打破平局的补充规则（tie-breaker）。通常，最简单的补充规则是优先选择编号最小的任务，或采用简单随机抽样方式进行抽取，有些任务优先规则也会明确列出特定的补充规则（Chen et al.，2018）。

不同的优先规则考虑的因素各不相同，基本可以分为以下几种类型（Klein，2000）。

1.基于项目网络的优先规则

基于项目网络的优先规则（network-based rule，NBR）利用的是传统的项目网络图中所包含的信息，但不考虑项目的资源信息。主要利用的信息有任务工期、紧后任务数量等。常见的基于网络的优先规则有：最短工期优先规则、最多紧后任务优先规则、最多后续任务优先规则等。

2.基于关键路线的优先规则

基于关键路线的优先规则（critical path-based rule，CPBR）是根据关键路线法的计算结果来选择任务，通常利用的信息包括任务的最早和最晚开始时间及最早和最晚完成时间。常见的基于关键路径的优先规则有：最早开始时间优先规则、最早完成时间优先规则、最晚开始时间优先规则、最晚完成时间优先规则、最小总时差优先规则等。

3.基于资源的优先规则

基于资源的优先规则（resource-based rule，RBR）关心的是任务的资源需求量。常用的基于资源的优先规则有：最大资源需求优先规则、最大资源使用优先规则等。

4.混合优先规则

混合优先规则（composite rule，CR）是为了避免过于关注单一信息。因此，经常将上述基于网络、关键路线及资源的若干优先规则结合起来，计算其加权和。Ulusoy和Ozdamar（1989）的研究证实，即使单个优先规则没有很好的调度效率，其合成的组合规则仍可能很有效。

表5.1列出了文献中常见的部分任务优先规则，这些规则主要用于具有常规目标函数的项目调度问题。表中第三栏表示该规则是选择优先值最大（max）的任务还是优先值最小（min）的任务。

表5.1　RCPSP常见优先规则

续表

续表

注：1.注意MTS与MIS的差异，在公式中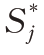表示任务j的后续任务集合。
2.在MINSLKD规则中，任务j的最早开始时间ESj（PS）是在SGS当前阶段根据已安排的部分进度计划（partial schedule，PS）及约束条件计算得到的。
3.RSM与WCS规则均只适用于PSGS，因为需要用到PSGS当前阶段的时间tg。
4.在WCS规则中，EShj（PS）表示PSGS根据当前的部分进度计划，如果从Dg中选择任务h的话，任务j最早可以开始的时间，其计算方法参见文献（Kolisch，1996b）。
5.WRUP是MAX MIS和MAX TRS规则的组合，根据Ulusoy and Ozdamar（1989）的计算分析，w=0.7是最佳取值。(www.xing528.com)

根据任务优先规则所需的信息是否为确定信息，可以将优先规则分为静态优先规则和动态优先规则（Klein，2000）。静态优先规则（static rule）需要的信息是确定的，只需要在调度开始之前计算一次优先值。动态优先规则（dynamic rule）所需的信息依赖于SGS的进展，因此每调度完一个任务，都需要重新计算候选任务的优先值。例如，表5.1中的MINSLKD就是动态规则。

此外，也可以根据优先规则所需信息的范围进行分类（Kolisch，1996b）。如果只需要候选任务自身的信息，则称为局部优先规则（local rule/myopic rule）；如果需要更多相关信息，则称为全局优先规则（global rule）。

当涉及多模式资源受限项目调度问题时，还需要有优先规则对任务执行模式进行选择（Boctor，1993）。对于资源受限多项目调度问题，一样可以采用SGS加优先规则的方法进行求解（Browning and Yassine，2010；Kurtulus and Davis，1982；Kurtulus and Narula，1985）。

对于具有非常规目标函数的RCPSP问题，尤其是RCPSPDCF问题，现有文献中的常用任务优先规则整理如表5.2所示。当然，很多表5.1中的优先规则，如MINSLK及MINLFT等，一样也可以应用于非常规RCPSP调度算法。

表5.2　非常规RCPSP的常见优先规则

注：1.在LSPPT规则中，MD表示当前已规划任务的最大延迟。
2.在IOCS规则中，TPj表示任务j延迟一个单位时间所增加的成本，即任务j的紧前任务对偶价格之和；ECj表示任务j的提前成本（earliness cost），即任务j的紧后任务对偶价格之和。对偶价格信息来自RCPSPDCF的对偶问题（Russell，1970）。

值得注意的是，由于SGS构造生成的是积极进度计划或非延迟进度计划，这些进度计划适用于常规目标函数，对于NPV等非常规目标函数并不是非常有效。因此，RCPSPDCF等非常规问题启发式算法往往增加了辅助算法来调整进度计划，例如正向逆向调度算法（Li and Willis，1992）就被很多学者用于RCPSPDCF的启发式算法中（Baroum and Patterson，1996）。

在上述的多项目进度生成机制中，已经可以看到多项目调度与单项目调度的差异。Kurtulus和Davis（1982）的研究表明，适用于单项目的优先规则，不一定适用于多项目调度。例如，在单项目调度中表现良好的SOF规则，在多项目调度中远逊于SASP这样的多项目调度规则。因此，在设计用于多项目调度的任务优先规则时，除了考虑项目网络、关键路线、项目资源，还需要考虑不同项目的相互影响。

表5.3列出了文献中部分常见的多项目调度任务优先规则，这些规则主要用于具有常规目标函数的多项目调度问题。

表5.3　多项目调度任务优先规则

续表

注：1.Ck为资源k的单位成本。
2.wi为项目i的权重，wi～[1，N]。
3.ACTIMij为任务（i，j）到该项目结束任务的最长路线长度。
4.LSSA规则事实上是MINLST与SASP的加权组合，w为0～1之间的权重系数。

当两项或多项候选任务的优先值相同时，需要打破平局的补充规则（tiebreaker），在多项目调度领域，常用的补充规则包括先到先得（first come first served，FCFS）规则（Dumond and Dumond，1993）与最大资源需求量（greatest resource demand，GRD）优规则（Kurtulus and Davis，1982）。假设当前均具有最佳优先值的候选任务集合为D0，则GRD规则定义为：

在现有文献中，对具有非常规目标函数的多项目调度问题研究相对较少。部分学者针对项目拖期惩罚和项目净现值提出了若干特定的任务优先规则（Chiu and Tsai，2002；Kurtulus and Narula，1985；Lawrence and Morton，1993）。鉴于多项目调度问题的特点，Lova和Tormos（2001）还提出一种两阶段优先规则，在第一阶段根据总工作量（TWK）规则选择项目，在第二阶段再根据最大资源需求（GRD）规则从中选择任务。

研究证实上述任务优先规则的表现取决于多项目特征参数（Browning and Yassine，2010；Kurtulus and Davis，1982；Kurtulus and Narula，1985；Kurtulus，1985）。因此，在能够事先估计多项目特征参数的情况下，也可以有针对性地选择特定的任务优先规则（Kara et al.，2001）。