上述统计检验结果和分析表明，几乎所有样本中小企业的权益资产收益率都在分析时段内出现了不同程度的跳跃现象。因此，对这些样本数据进行研究时，基于纯扩散的违约风险测度方法将会造成违约风险的普遍低估。为了对此进行验证，分别利用基于纯扩散过程的信用结构模型和基于跳-扩散过程的信用结构模型求得企业违约距离[6]，然后将两种违约距离的差值与峰度及偏度进行比较，结果如图9.1和图9.2所示。
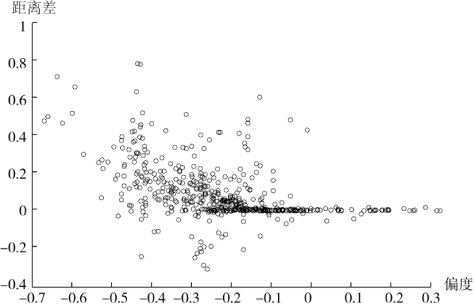
从图9.1可以看出，当偏度值位于-0.25～0.25之间时，两种方法估计的违约距离差较小，甚至没有明显差异，这说明，当权益资产收益率的负偏度绝对值不大或负的极端值出现较少时，利用纯扩散模型来测度违约风险对违约风险低估并不严重。但是，当偏度降至-0.25以下时(表9.1显示约50%企业偏度小于-0.25)，利用纯扩散模型来测度违约风险，低估问题将逐渐变得比较严重。对于有些负偏度绝对值较大的企业，两种方法估计的违约距离差甚至达到0.7以上。
从图9.2可以看出，当峰度值小于3.25时，两种方法估计的违约距离差较小，基本上在-0.2～0.2之间，这说明，当资产收益的峰度较接近正态分布的峰度3时，无论是用纯扩散模型还是用跳-扩散模型度量违约风险，其差异均较小。但是，当峰度增加至3.25以上(表9.1显示90%以上的企业峰度大于3.25)，尤其是4以上时，厚尾现象明显，极端值增加，纯扩散模型将对违约风险显著低估。
(www.xing528.com)
图9.1 两种方法求得的违约距离差与偏度的关系图
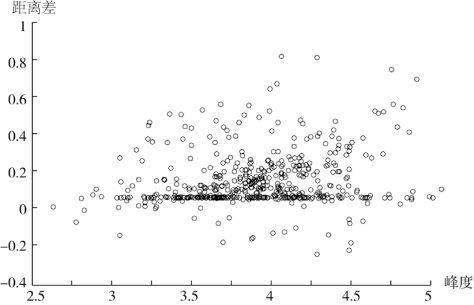
图9.2 两种方法求得的违约距离差与峰度的关系图
通过上述分析不难发现，当企业权益资产收益分布峰度和偏度明显偏离正态分布的峰度和偏度时，跳跃频率和幅度将较为显著，从而对违约风险产生较大的影响，这和Zhang等(2009)的结论是一致的。此时，如果使用基于纯扩散过程的测度方法对违约风险的估计会有明显偏误。而基于跳-扩散过程的测度方法则不仅考虑了跳跃现象出现时违约风险的变化，而且当跳跃因子的跳跃频率或跳跃幅度为0(实践中近似为0)时，它将会退化为纯扩散模型。这意味着，即使在跳跃现象不明显时，跳-扩散模型对违约风险度量的偏差也会较小。因此，跳-扩散模型更适用于度量中小企业的违约风险。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
