了解Black-Scholes期权定价方法

为了能根据基础资产价格(如股票)导出期权定价公式，Black和Scholes(1973)首先给出了以下假设条件:

(1)在期权有效期内，短期利率r是取值为常数的无风险利率；

(2)股票价格遵循纯扩散过程: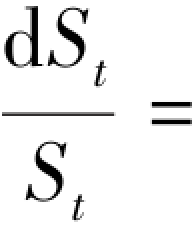μSdt＋σSdBt^[1]，其中μS和σS为常数；

(3)股票在期权有效期内不支付红利；

(4)所考察的期权为欧式期权，即只能在到期日执行，执行价格为K；

(5)买卖股票和期权都没有交易成本；

(6)允许对股票进行卖空交易，且所有股票都是完全可分的，交易具有连续性；

(7)投资者可按无风险利率无限制地借贷以进行股票买卖。

(2)和(6)表明标的资产(股票)的变化过程是连续而均匀的，不存在突然的跳跃，其他的假设条件则保证市场为有效市场，不存在无风险套利机会。(www.xing528.com)

在上述假设下，Black和Scholes(1973)利用了无套利方法对期权定价公式进行了推导，该方法的要点如下:

首先，令期权价格为标的资产(股票)的函数Ct＝f(St，t)。

其次，构造一个资产组合:持有一份买入期权，并卖出n份股票。记该资产组合的价值为It＝Ct-n·St，那么根据定理2.4有:

然后，对于该无风险资产组合，其瞬间收益率就应该等于无风险利率r，因此有:

最后，由两种方式求得的瞬间收益率应该相等，所以由式(5.4)和式(5.5)得:

因此，在边界条件“t＝T时有f＝max(ST-K，0)”下解该偏微分方程可得B-S期权定价公式:

B-S期权定价公式给出的价值只与股票的现价、股票波动率、期权执行价格、到期期限及无风险利率有关，而与期望收益率μS无关，这表明风险的中性。也就是说，期权的合理价格与人们的风险偏好无关。因此，B-S公式使用起来非常方便，降低了期权定价的难度与不确定性。

在构建了B-S(Black-Scholes)期权定价公式以后，Black和Scholes(1973)也提到企业负债问题可以转换为期权定价问题，不过并未就此问题进行深入的探讨。Merton(1974)则以欧式看涨期权定价理论为基础，对企业权益和债务定价问题进行了较为全面和深入的探讨，构建了违约风险的结构化模型，在若干方面对Black和Scholes(1973)作了重要推广，开创了信用风险理论和实证研究的新思路，使违约风险度量的实证研究有了突破性的进展。