TSD-ARJI-GARCH模型预测能力验证

为了对模型的预测能力进行评估和比较，首先选取2003—2008年权益资产收益数据作为样本内观测值，分别利用TSD-ARJIGARCH模型、ARJI-GARCH模型、ARJI模型和CJI模型对其进行拟合分析，并对各模型中的参数进行估计。然后，再选取2009年的权益资产收益数据作为样本外预测值，对前述模型预测能力进行检验。

现以金健米业为例，先分别利用四个模型对其2003—2008年数据进行拟合分析，再利用得到的估计模型对其2009年跳跃风险进行预测分析。图4.12为金健米业在2009年期间的日收益率时序图。图4.13～图4.16分别为依据四个不同模型得到的金健米业在2009年间的日收益率跳跃强度预期值和发生跳跃的事后概率。

TSD-ARJI-GARCH模型和ARJI-GARCH模型的共同特点是将可变强度和GARCH过程结合起来，既考虑了跳跃行为中的可变特征和集群效应，又考虑了扩散型条件波动率的GARCH效应以及它对好坏消息的不对称反应。对比图4.12和图4.13、图4.14可以看出，TSD-ARJI-GARCH模型和ARJI-GARCH模型都较好地预测了2009年金健米业权益资产日收益率中的大幅跳跃，较为准确地识别了跳跃发生的时点和跳跃强度发生变化的时间区域。

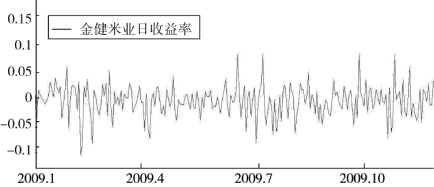
图4.12　金健米业2009年日收益率时间序列图

反观ARJI模型，因为将扩散型条件波动率视为常数，仅对跳跃强度的变化作出了解释，因此普遍存在着高估跳跃强度的现象，进而导致跳跃发生的概率偏大，对收益率跳跃变化的预测明显较差，这一点可以由图4.15得以验证。而CJI模型则将跳跃强度和扩散型条件波动率都视为常数，完全没有考虑跳跃行为和正常扩散波动的各自特点，所以其预测和识别能力最差。从图4.16可以看出，该模型估计的跳跃强度完全不能预测跳跃行为的变化特征，且跳跃发生的事后概率也与实际情况有一定偏差。

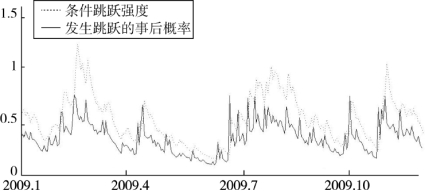
图4.13　TSD-ARJI-GARCH模型的预测图

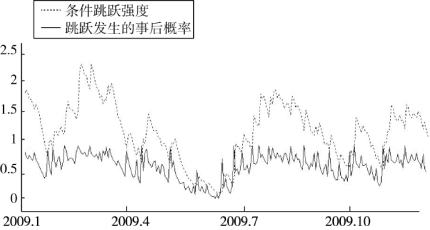
图4.14　ARJI-GARCH模型的预测图

由于TSD-ARJI-GARCH模型和ARJI-GARCH模型对跳跃行为的特征都作出了较为准确的预测，因此仅比较这两个模型对条件跳跃强度和事后发生跳跃概率的预测，很难判断它们预测能力孰优孰劣。下面将分别用这两个模型分析金健米业权益资产收益的总条件方差及其GARCH成分和跳跃成分，然后比较哪个模型能更好地描述扩散风险和跳跃风险的变化特征。

根据ARJI-GARCH模型估计参数计算的条件总方差、GARCH成分和跳跃成分如图4.17所示，从该图中可以发现，GARCH成分与条件总方差变化模式完全一样。日收益率出现的非经常性大幅波动的特征几乎全部反映在GARCH成分中，而跳跃成分并不十分明显，这显然是该模型将部分跳跃成分错误地识别为GARCH成分。

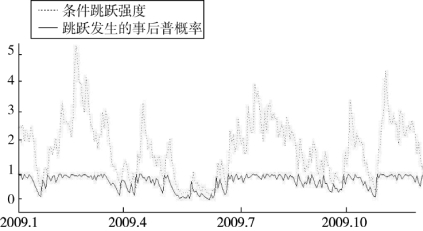
图4.15　ARJI模型的预测图

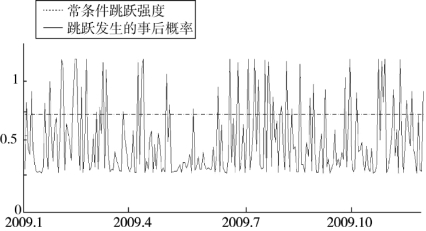
图4.16　CJI模型的预测图

图4.18则是根据TSD-ARJI-GARCH模型估计参数计算的条件总方差、GARCH成分和跳跃成分。模型TSD-ARJI-GARCH与ARJI-GARCH的差异在于，前者考虑了A股指数前期波动对跳跃预期的影响。

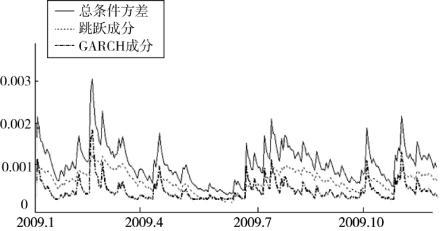
图4.17　基于ARJI-GARCH模型的总条件方差、跳跃成分和GARCH成分

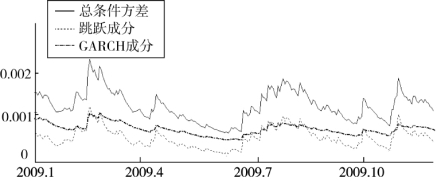
图4.18　基于TSD-ARJI-GARCH模型的总条件方差、跳跃成分和GARCH成分(www.xing528.com)

从金健米业的日收益率与A股指数的日波动率对照图4.19可以看出，在A股指数发生较大波动的时间点及其之后的一段时间内，金健米业日收益率的跳跃强度几乎都出现了变化，两者之间反映出很强的相关性。因此，在权益收益率跳跃行为的模型中加入A股指数波动会改善模型的解释和预测能力。由于考虑了A股指数前期波动对跳跃预期的影响，图4.18中的GARCH成分较好反映了总体条件方差中经常性、平滑的波动，而跳跃成分则描述了非经常的大幅波动。因此，总方差成分分析表明TSD-ARJI-GARCH模型比ARJI-GARCH模型有更好的预测能力。

为了更好地比较模型的预测能力，并检验其稳健性，接下来将利用所有样本企业2009年的权益资产收益进行预测检验。由于大量的实证文献已经验证了ARJI-GARCH模型是对原有两种模型的改进，所以仅需比较ARJI-GARCH模型和TSD-ARJI-GARCH模型的预测能力。

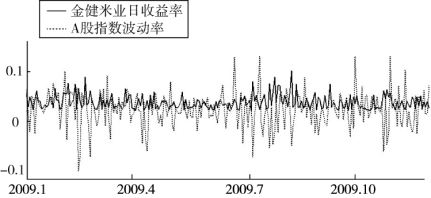
图4.19　金健米业的日收益率与A股指数日波动率对照图

首先借鉴Maheu和Mccurdy(2004)的方法进行预测能力的评价。Maheu和Mccurdy(2004)将预测值对实际变量值进行回归分析，然后利用拟合度R2的大小来度量模型的预测能力。因此，先对权益资产日收益率的波动进行回归分析:

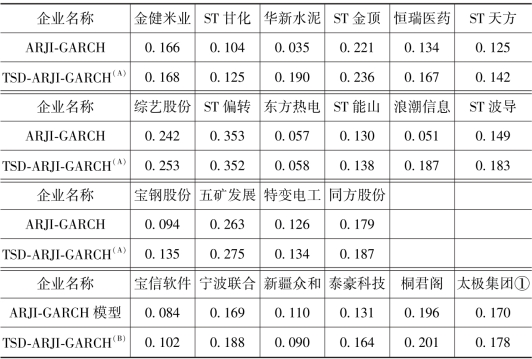
在进行模型预测时，随着新信息的不断到来，每隔一段时间需要更新参数的估计值，但计算量将会非常庞大(Maheu和Mccurdy，2004)。由于我们的主要目的仅仅是比较ARJI-GARCH模型和TSDARJI-GARCH模型预测效果，而不是进行精度要求较高的预测，所以为了避免大量计算的复杂性，仅根据2003—2008年数据估计的参数值来比较两模型在短期内的预测能力，预测样本为2009年1月—2009年6月。现分别利用两种模型进行参数和总条件方差估计后，依据Maheu和Mccurdy(2004)的方法进行回归分析，得到的拟合度R2见表4.4。

表4.4　ARJI-GARCH模型和TSD-ARJI-GARCH模型的预测能力比较

①由于模型估计和参数估计都发现“桐君阁的权益资产收益波动”对太极集团的跳跃预期有明显影响，加入该状态变量后模型的极大似然值高于以“A股指数收益波动”作为状态变量的模型估计似然值，状态变量参数的显著性也明显提高，因此在考察预测能力时选择了“桐君阁的收益波动”作为影响太极集团跳跃预期的状态变量。

预测检验的结果表明，对大多数企业而言，在强度估计式中加入系统波动或者关联波动等状态变量，对模型有明显的改善作用。TSD-ARJI-GARCH模型在大多数情况下对已实现波动率拟合度R2更高，预测能力更强。

为了进一步验证该结论的稳健性，再使用近来较为流行的高级预测能力检验法(SPA检验)来比较两种模型的预测效果。国内一些文献都使用了该方法来比较各种模型的预测效果，如魏宇和余怒涛(2007)及方立兵等(2010)。由于这些文献都对该方法作了详尽的介绍，因此，关于该方法的具体检验步骤不再赘述。此处SPA检验所采用的主要是以下四种损失函数:

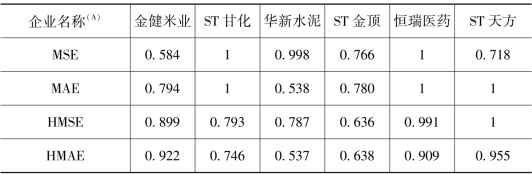
检验中的基础模型为TSD-ARJI-GARCH模型，检验的零假设为“H0:TSD-ARJI-GARCH模型预测能力最优”。SPA检验结果(即p值)见表4.5，p值越大(越接近1)，表示TSD-ARJI-GARCH模型预测能力越优于ARJI-GARCH模型。

SPA检验结果也表明，在4种损失函数情况下，TSD-ARJIGARCH模型预测能力基本上都优于ARJI-GARCH模型。这进一步验证了在ARJI-GARCH模型中加入状态变量的门限效应是很有必要的，将有助于提高模型预测能力。

表4.5　基于对已实现波动率SPA检验的模型预测效果比较

续表

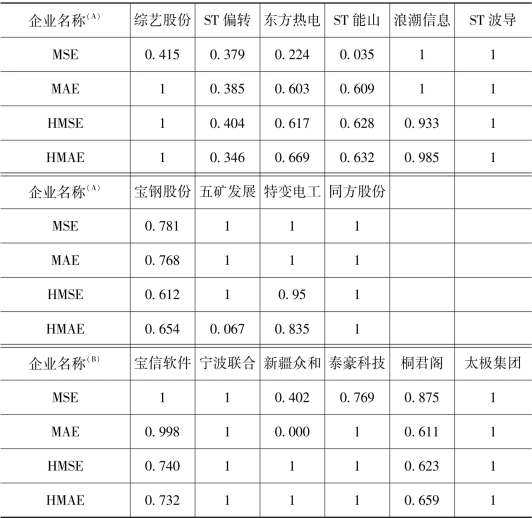
注:(A)表示状态变量为“A股指数收益率波动”，(B)表示状态变量为“关联企业权益资产收益率波动”。