现以金健米业为例，利用TSD-ARJI-GARCH模型讨论单个企业权益资产的跳跃特征。图4.3为金健米业2003年1月至2008年12月权益资产日收益率的时间序列图。其收益率在2003—2006年期间跳跃频率较低，大幅跳跃并不常见。而2007—2008年由于受到美国金融危机，我国雪灾、地震等突发事件影响，大幅波动次数和幅度都明显增加。常数跳跃强度显然不能描述这些变化特征。
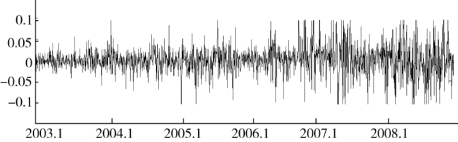
图4.3 金健米业日收益率时间序列图
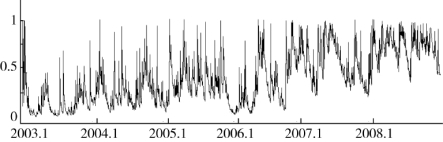
图4.4为条件跳跃强度时间序列图，从图中可以明显看出条件跳跃强度的时变性和集群性。而图4.5为企业权益资产收益率发生跳跃的事后概率，即
，它是对跳跃发生的事后识别和推断。对比图4.4和图4.5可以发现:
图4.4 金健米业条件跳跃强度
(www.xing528.com)
图4.5 金健米业发生跳跃的事后概率
(1)在权益资产收益率出现大幅跳动的时段上，条件跳跃强度明显增加，预期了更大的跳跃频率和跳跃风险。而在权益资产收益率波动较小的时段上条件跳跃强度明显减小，降低了对跳跃风险的预期。这说明模型的预期与跳跃点的出现、跳跃风险的增加较为一致。
(2)权益资产收益率较大的波动基本上都能被较大的事后概率识别，说明模型能对权益资产收益率的大幅波动和跳跃变化作出较为准确的判断。
(3)条件跳跃强度(跳跃发生前的预期)与跳跃事后概率(跳跃发生后的识别)的变化基本上是一致的，即较大的条件跳跃强度，对应的跳跃事后概率较大；较小的条件跳跃强度，对应的跳跃事后概率也较小。这说明对跳跃变化出现的事前预期基本上都得到了事后的验证。
现利用ARJI-GARCH分析金健米业权益资产发生跳跃的事后概率，并与TSD-ARJI-GARCH模型分析结果进行对比，结果如图4.6所示。通过对比可以发现，TSD-ARJI-GARCH模型能更好识别跳跃行为。如果将超过均值±1.64标准差的日收益率视为跳跃(共有217个跳跃点)，并以概率大于0.5为标准来识别跳跃，TSDARJI-GARCH模型几乎识别了所有跳跃，且较好地区分了跳跃与非跳跃变化(犯第一类错误的概率为0.005，犯第二类错误的概率为0.212)。而ARJI-GARCH模型虽然也识别了所有跳跃点，但是对非跳跃点存在着严重的过度识别(犯第一类错误的概率为0.005，犯第二类错误的概率为0.498)，将许多小幅波动都识别为跳跃，分辨能力较低。这应该是因为TSD-ARJI-GARCH模型从全部信息中分离出了状态变量对跳跃强度的影响，从而减轻了模型的过度识别。
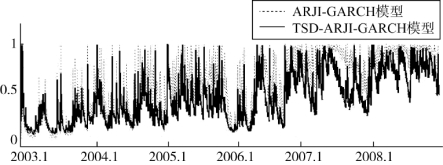
图4.6 基于不同模型的跳跃发生事后概率对比图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
