模型估计和检验方法

首先，分别利用四种模型，即常跳跃强度模型(简称CIJ模型，有β1＝β2＝β3＝0，ω1＝ω2＝ω3＝0)、自回归强度模型(简称ARJI模型，有β3＝0，ω1＝ω2＝ω3＝0)、自回归强度混合GARCH模型(简称ARJI-GARCH模型，有β3＝0)和门限效应下状态变量依赖自回归强度-GARCH模型(简称TSD-ARJI-GARCH模型)。对前述22家企业权益资产的日收益率进行估计，求出各模型估计的对数似然值。然后，利用似然比(LR)检验和赤池信息值(AIC)来判断各模型的拟合优度，统计检验结果见表4.2。

利用TSD-ARJI-GARCH模型进行估计时，选取股票市场收益波动率^[3](用A股指数收益率的绝对值表示)作为状态变量时，是考察市场波动对单个企业权益资产跳跃强度影响的“系统效应”，而选择交叉持股企业权益资产收益波动率(用其收益率的绝对值表示)作为状态变量时，是考察关系密切企业间大幅波动的“传染效应”。

关于门限值K的取值作如下处理:考察“系统效应”时，门限值K分别取A股指数1997—2002年日波动率标准差的0倍(表示无门限效应)、0.5倍、1倍和1.5倍；考察“传染效应”时，K分别取交叉持股企业从上市日至2002年日波动率标准差的0倍(表示无门限效应)、0.5倍、1倍和1.5倍。经比较发现:(1)对于大多数企业而言，K为0时，状态变量对跳跃强度影响不显著，而K取其他值时，这一情况发生变化。这说明状态变量对企业权益资产收益率跳跃强度的影响具有门限效应，只有当波动达到一定的水平才会对单个企业跳跃强度产生明显影响；(2)选择1倍标准差作为区别大小波动的门限值时估计效果最优，且状态变量基本都在5%～10%水平上显著。因此，表4.2中列出的TSD-ARJI-GARCH模型估计值是取K为1倍标准差的情况下得到的。

表4.2　四种模型的对数似然值、赤池信息值(AIC)和部分LR检验值^[4]

续表

注:对数似然值下括号内为模型估计的AIC值，LR检验值下括号内为p值。

根据表4.2所示的各模型AIC值和LR检验结果可以得到以下几个结论:

(1)研究权益资产收益率发生跳跃的强度模型从最初的CIJ模型变化为可变强度模型时，对数似然值出现相当明显的增加且AIC值全部减小。经似然比检验，所有的可变强度模型都在5%的显著水平上拒绝了CIJ模型。这表明资产收益率的跳跃强度随时间发生变化，并具有明显的集群效应。

(2)将ARJI模型与ARJI-GARCH模型进行比较时，大部分权益资产都在10%水平上拒绝了ARJI模型，而接受ARJI-GARCH模型。这说明将GARCH模型和可变强度模型结合起来有助于改善模型的解释能力。(www.xing528.com)

(3)TSD-ARJI-GARCH模型的对数似然值最大，AIC信息值最小。对TSD-ARJI-GARCH模型和ARJI-GARCH模型及ARJI模型进行比较时，似然比检验结果表明，几乎所有的样本值都在5%～10%的显著水平上拒绝了ARJI-GARCH模型和ARJI模型。这说明单个资产的跳跃强度不仅受自身特质因素的影响，而且也会随状态变量信息的变化而出现调整。在单个资产的条件跳跃强度估计模型中引入状态变量，会明显改善模型的估计效果，弥补现有模型的不足。

(4)ST企业的跳跃方差明显大于同行业的非ST企业跳跃方差，跳跃特征更显著，跳跃风险更大。

(5)持股企业和被持股企业间波动的传染性是单向的。“持股企业收益波动率”大幅变动对“被持股企业”的跳跃变化有显著影响，而“被持股企业收益波动率”大幅变动对“持股企业”跳跃变化的影响较小。

从上述分析不难看出，TSD-ARJI-GARCH模型在刻画权益资产收益率跳跃强度的时变特性和集群现象方面具有明显优势。现利用TSD-ARJI-GARCH模型估计各企业权益资产收益率的参数，所得估计值如表4.3所示。后续将根据此表分类讨论各企业权益资产收益率的跳跃变化特点、ST企业和非ST企业的不同波动风险特征以及交叉持股企业间大幅跳跃的传染性。

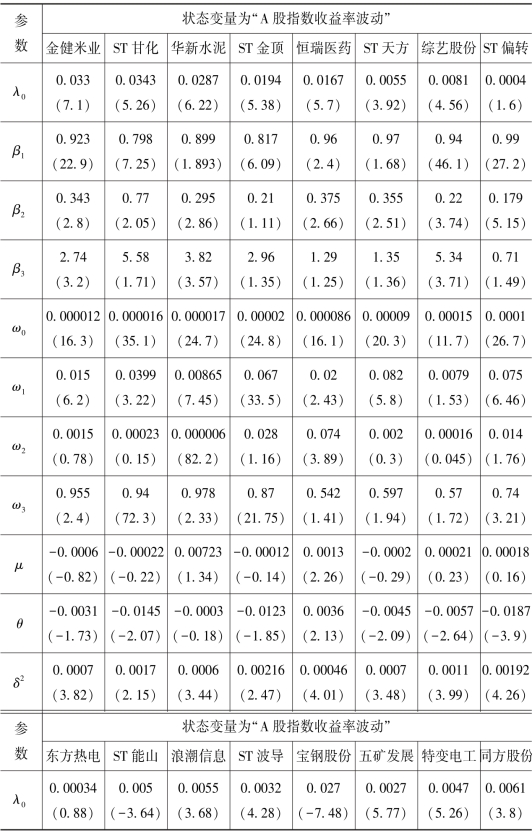
表4.3　基于TSD-ARJI-GARCH模型的参数估计值

续表

续表

注:括号内为参数估计的t值。