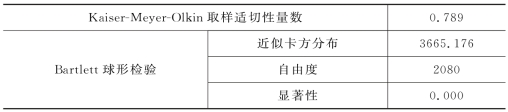
建构效度(Construct Validity)是测量出理论的概念或特质的程度,简言之,就是对某一特质能够解释多少,对量表建构效度的检验是通过因素分析——探索性的因素分析(Exploratory Factor Analysis)。其检验过程首先要通过取样适切性量数(Kaiser-Meyer-Olkin measure of sampling adequacy,KMO)与Bartlett’s的球形检验来判断数据是否适合做因素分析。依据Kaiser(1974)[4]的观点,KMO是介于0~1的数值,当KMO<0.5时,表示题项间不适合做因素分析;KMO≥0.9表示极适合因子分析;KMO≥0.8表示适合,KMO≥0.7表示题项变量间尚可进行因素分析,同时Bartlett’s的球形检验结果具有显著性,证明适合进行因素分析。然后,通过主成分分析和转轴法抽取共享因素,以方差最大正交旋转法对初始因子进行旋转。最后,利用因子负荷系数判断是否符合要求。因子负荷系数的选择标准以Lederer和Sethi(1991)[5]提出的观点为基础,认为若因子负荷系数<0.5或存在两个构面下因子负荷系数均大于0.5的情况时,均应删除。借助SPSS 22对预试问卷进行因素分析,如表7-5所示,KMO值为0.789,Bartlett’s的球形检验具有显著性,适合进行因素分析。KMO值不高主要是预试问卷调研的样本量规模较小,正式问卷时获取大样本后指标数值会有所提高。
表7-5 KMO与Bartlett检验
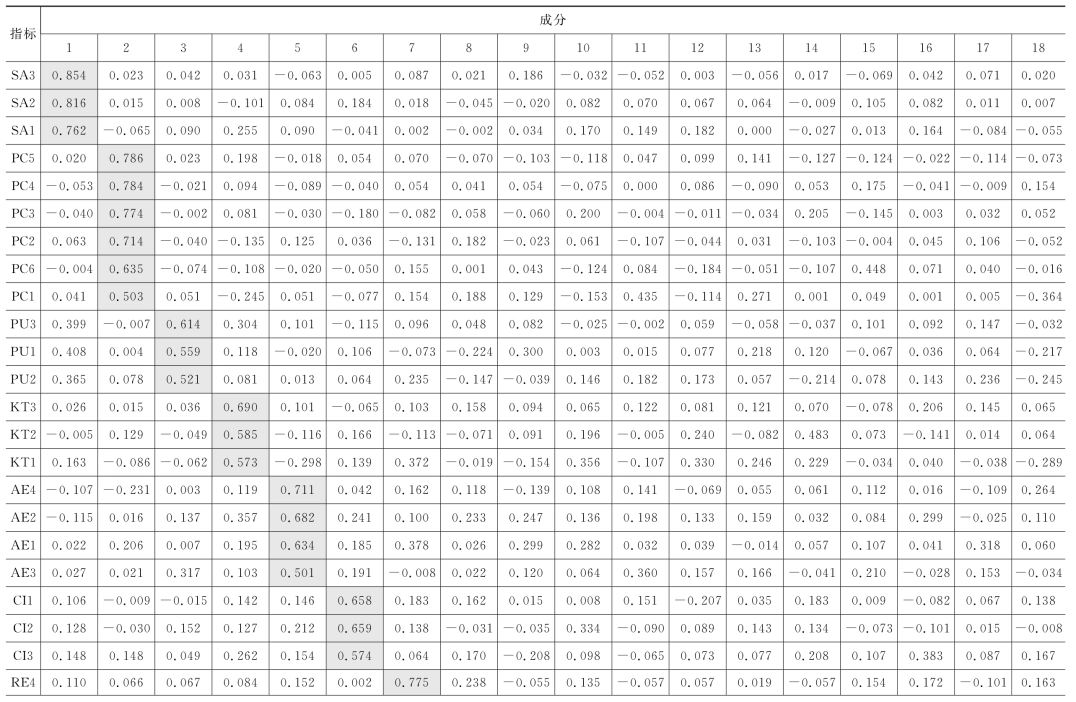
经过方差最大正交旋转后,得到结果如表7-6所示,66个测量题项经过19次迭代收敛共提取出18个共同因素,可解释77.912%的变异量。各因素构念与初始编制问卷的构念吻合,说明各维度具有较好的区分度。各变量的因子负荷系数均大于0.5,尽管有部分变量的因子负荷系数刚刚超过0.5如PC1、AE3,但本书考虑预试调查样本量较小造成系数值不高。
表7-6 预测问卷旋转后因子负荷(https://www.xing528.com)
续表

续表

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




