1.遗传算法典型算例
虽然遗传算法在不同模型中的适应度函数是不同的,但其基本的操作流程大体一致,包括编码和初始种群的生成、种群中个体适应度的检测与评估、选择、交叉、变异。下面给出一个含有两个优化目标的多目标函数优化问题解法[167],其他单目标函数可以参照实现。


程序运行结果如图7.33、图7.34所示,图中位于上方的曲线代表种群平均值的变化,下方曲线代表优化结果的变化,可以看出经过100次迭代后两个目标函数都取得了较好的优化结果,其中第一目标函数值在1.2左右,第二目标函数值在3.02左右。

图7.33 第一目标函数优化结果和平均值变化曲线图
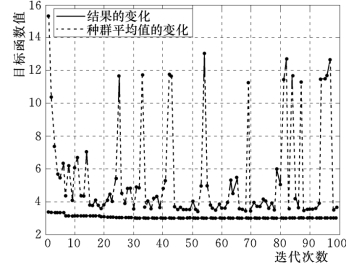
图7.34 第二目标函数优化结果和平均值变化曲线图
以上是基本遗传算法的实现,需要结合遗传算法工具箱进行计算,其中的适应度函数可根据具体的模型进行改变,但实现的基本思路是相通的。除了以上借助遗传算法原理进行编程外,在Matlab7.0的工具箱中包含了遗传算法GUI,利用GUI可以更快、更方便地实现遗传算法的计算和优化。
2.遗传算法GUI实现
在使用遗传算法工具箱GUI之前,首先需要编写一个.M文件,来确定想要优化的函数。该.M文件可接受一个行向量,并且返回一个标量。行向量的长度就是目标函数中独立变量的个数。
例如想要计算如下函数的最小值:
![]()
如式(7.3),函数是关于三个变量的表达式,那么.M文件确定这个函数必须接受一个长度为3的行向量,分别与变量x1、x2、x3对应,并且返回一个标量Y,Y的值即为函数的值。计算该函数最小值的.M文件代码如下:
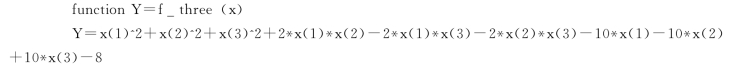
此外,需要注意的是遗传算法工具箱中的优化函数总是使目标函数或适应度函数最小化,如果想得到函数的最大值,只需做一个简单的变换,令新的F(x)=-f(x),再按照上述方法建立相应的.M文件,进行计算。
有了上述的.M文件,即可在Matlab7.0中调用命令“gatool”,使用遗传算法GUI进行计算。(https://www.xing528.com)
在Matlab运行框中输入“gatool”,出现如图7.35所示界面。
在进行遗传算法之前,需要对适应度函数和变量个数进行定义,这里的变量个数是指适应度函数的独立变量个数。本例利用上述建立的f_three函数作为适应度函数,显然变量个数为3。

图7.35 遗传算法GUI
在图7.35所示工具箱的“Fitness function”和“Number of variables”中分别输入“@f_three”和“3”,然后点击“Start”按钮进行计算,当算法完成时,在“Status and results”中出现如图7.36所示的结果。
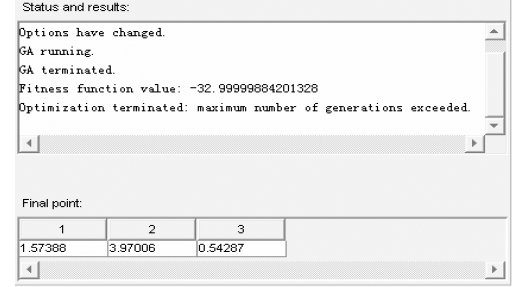
图7.36 经过100次迭代后的计算结果
由图7.36所示的状态和结果可知,算法终止时适应度函数的最终值为:-32.99999884201328,经过默认的100迭代后,算法的最终点为[1.57388,3.97006,0.54287]。
如果想得到遗传算法的每一代适应度函数的最佳值和平均值的图形,那么可以通过图7.35中的“Plots”来实现,在“Plots”中选择“Best fitness”,然后点击“Start”按钮,出现如图7.37所示的最佳值和平均值。

图7.37 适应度函数的最佳值和平均值
从图7.37中可以看出,函数当前代的最佳值为-33,平均值为-32.9983;图中上方的点表示平均适应度值,下方的点表示最佳适应度值,很明显,结果达到了非常高的精度。为了更清晰地显示每一代的迭代结果,还可以将图7.37的纵坐标设置为对数坐标。
同时,也可以将Matlab自带的常用的Rastrigin函数作为适应度函数,其变量个数为2,函数表达形式如下:
![]()
在图7.35所示工具箱的“Fitness function”和“Number of variables”中分别输入“@rastriginsfcn”和“2”,然后点击“Start”按钮进行计算。当算法完成时,在“Status and results”中出现计算后的结果。算法终止时适应度函数的最终值为0.006011332101213185,经过默认的100迭代后,算法的最终点为[-0.0055,0.00024]。
同样,如果想得到遗传算法的每一代适应度函数的迭代过程和最佳值点的图形,可以通过图7.35中的“Plots”来实现,在“Plots”中选择“Best fitness”与“Best individual”,然后点击“Start”按钮,出现如图7.38所示图像。
以上是两个典型且通用的遗传算法实现的例子,用户可根据自身需要进行定义并计算复杂的模型,同时通过Delphi与Matlab的交互,更好地实现需求。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




