应用神经网络预测未知风险元传递模型

图6.33　2005年5月～2007年12月实际负荷分布图

为了验证算法的有效性和准确性，这里主要对PIC中关键因素之一的电力负荷进行预测。以中国东部某省网2005年5月～2007年12月的月最大统调用电负荷数据（见图6.33）为依据，考虑当地影响负荷的气象数据，如温度、湿度等，并将这些因素对负荷影响的专家评估值作为URNN的未确知风险元输入变量。分别用传统的时间序列模型ARIMA、BP神经网络模型（BPNN），以及本书所列的URNN模型，对负荷进行预测。在预测的过程中，一方面利用2005年5月～2007年6月数据对2007年7～12月的负荷进行预测，并进行误差分析，比较三个预测方法的预测精度；另一方面，根据2005年5月～2007年12月数据，利用预测精度最高的模型对2008年上半年的负荷进行预测，并通过2008年前4个月的最新观察数据，进行误差分析。

本实例数据分析计算机（AMD Athlon X2 1.8G，2048M memory）操作系统为Windows Vista，预测平台为Matalb7.0，同时利用SPSS13.0对数据进行初始化处理和时间序列分析（ARIMA分析）。在进行神经网络计算时，对BPNN和URNN的训练次数都为1000，神经网络的隐含层函数都设置为sigmoid函数，输出函数为线性函数，输出为一个节点。此外，对输入数据进行标准化的表达式如下：

式中：x（t）是t时间的实际值；x′（t）为经过标准化后的负荷值；xmax（t）为实际负荷的最大值；xmin（t）为实际负荷的最小值。

为了度量模型的预测精度，给出算例中的三个误差定义：相对误差ER、标准偏差ESD、均方根误差ERMS，设x（t）是t时间的实际值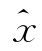，（t）是t时间的预测值，n是需要预测的数据个数，则三个误差的表达式为：

以2005年5月～2007年6月数据为依据，利用ARIMA模型、BPNN模型和URNN模型对2007年7～12月的负荷进行预测，并进行相应的误差计算，得到如表6.18所示的负荷预测数据。

通过表6.18可以看出，BPNN的预测数据比ARIMA模型更接近实际负荷数据，虽然ARIMA考虑了负荷数据的季节性变化，但BPNN能根据网络的不断训练，使预测精度提高；而URNN的预测数据显然要比BPNN模型更接近实际数据，这是因为在构建神经网络中，不仅考虑了风险因素的影响，而且网络是一种递归结构，可以对输入数据进行去噪音处理。

表6.18　使用三种不同的算法对2007年7～12月负荷进行预测的结果

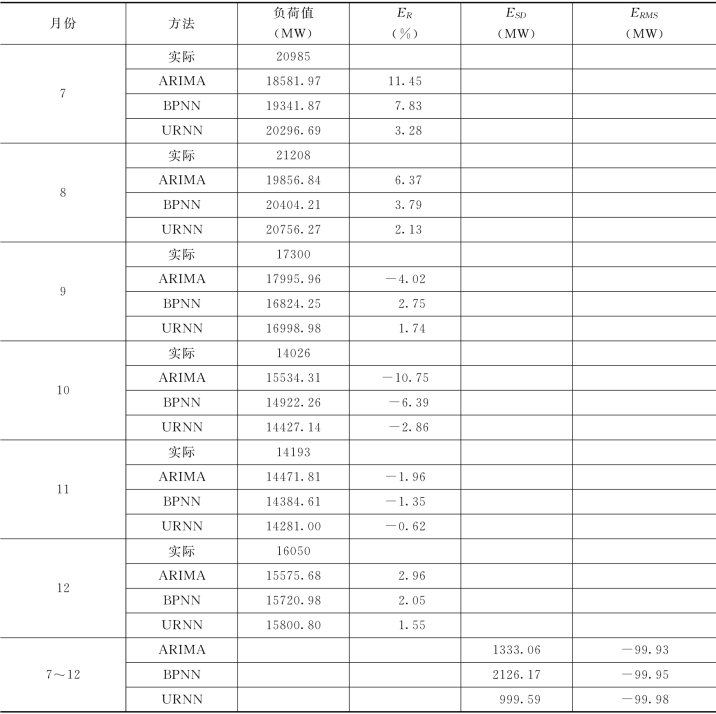
通过计算三种模型的相对误差，发现URNN的相对误差最小，例如在2007年8月的预测中，ARIMA的ER为6.37%，BPNN为3.79%，URNN为2.13%，可见URNN模型的预测精度最高，BPNN其次。此外，表6.18还给出了三种模型的标准偏差和均方根误差，BPNN的ESD最大，说明BPNN预测的数据波动性较大，网络结构需要进行改进；而均方根误差的大小直接用来衡量预测精度的大小，该误差以100为准点，其绝对值越接近100说明模型的预测精度越高，从表6.18可以看出，URNN比BPNN的预测精度高3%，比ARIMA要高5%。三种模型对2007年7～12月的预测曲线，如图6.34所示。(www.xing528.com)

通过以上分析，可以看出URNN模型具有较好预测效果。利用2005年5月～2007年12月负荷数据对2008年前6个月的负荷进行预测，图6.35是相应的负荷预测曲线及实际负荷曲线，表6.19是相应的负荷预测数据及实际负荷数据。通过计算得出前4个月的平均相对误差约为2.59%。

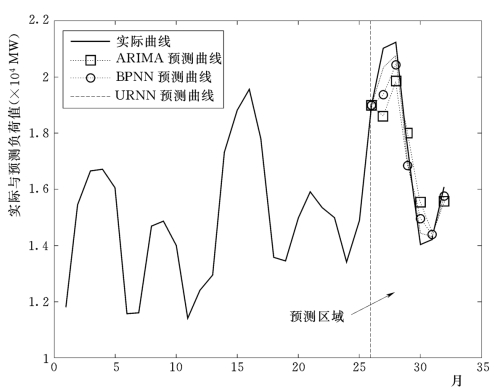
图6.34　2007年7～12月负荷预测曲线

图6.35　2008年1～6月负荷预测曲线（URNN）

表6.19　使用URNN模型对2008年1～6月负荷进行预测的结果及实际负荷数据

综上可以看出，利用未确知数学对风险元进行重定义，建立相应的电力智能中心的神经网络负荷预测模型具有以下几个特点：

（1）将广义项目风险元根据不确定信息类型进行分类，提出了四种基本的传递路线，为处理电网规划中的不确定信息奠定了基础。

（2）建立了一种新的动态联盟协同决策模型，提出了电力智能中心的全新概念，结合风险元传递理论，将发电部门、输电部门、配电部门、客户四者结合起来，应对电网规划中的各种风险影响。

（3）给出了未确知风险元的一系列数学定义及其操作，依据这些操作结合Elman's递归神经网络建立了新的负荷预测模型。实例结果表明，该模型不仅使模型预测精度提高，而且比传统的预测方法的预测精度更高，为PIC处理风险影响提供了保障，使模型更加符合实际需求。

（4）当受随机、模糊、灰风险元影响时，PIC需要结合其他智能工具进行具体分析，而将这三者结合的盲信息[175]处理，是将来需要进一步研究的工作。