基于未知风险元素的递归神经网络预测模型

递归神经网络有一个或多个反馈循环，Elman's递归神经网络是其中一种，它与其他递归神经网络相比有很好的处理能力，此处以Elman's递归神经网络结构为基础，将未确知风险元引入结构，得到新的基于未确知风险元的递归神经网络预测模型（URNN）。

URNN网络包含一个递归联系层，这个层由从隐含神经元到衔接单元层组成。这些衔接单元存储了隐层神经元的输出单元，同时衔接层将输出单元可以反馈至输入单元。此外，URNN结构的输入层包含两部分，一部分是需要预测的数据，另一部分是PIC中所受未确知风险元的大小，这些未确知风险元可以按照如下的转化关系，将实数表示的风险元转化为未确知数表示的风险元。

根据参考文献[174]，规定：

实数集用R表示，而全体未确知数构成的集合用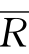表示，则对任意a∈R，令a对应于的未确知数{[a，a]，Fa（t）}，即：a↔{[a，a]，Fa（t）}。这一对应关系用K表示，未确知数{[a，a]，Fa（t）}的数学操作和5.3节定义的操作完全相同。那么，基于URNN模型的电力智能中心处理后台如图6.32所示。

图6.32　基于URNN模型的电力智能中心处理后台

在图6.32中，xi（t-1）表示在进行递归神经网络处理前的第i个待预测数据，{[ri，ri]，（t）}表示第i个未确知风险元，wai，j表示第i个待测节点到隐含层第j个节点的权重，表示第i个未确知风险元到隐含层第j个节点的权重，zi（t）表示经过加权和未确知风险处理后的第i个待预测数据，Φ表示神经网络的处理函数，可以是Sigmoid或线性函数，xi（t）表示完成递归网络处理后的第i个待测数据，wb′i表示从隐含层到输出层之间第i个节点的权重，s（t）表示加权后的函数，y（t）表示预测数据或向量。图6.32中变量的数学表达关系表示如下：

式中：代表相应数据的平均值。

由于在URNN中，输出层没有信息反馈，那么该层权重的标准误差可以修订如下：

(www.xing528.com)

式中：μ为步长参数；e（t）为标准误差。那么，对于隐含层，误差修订如下：

如果令，表示状态变量xk（t）的偏导数，那么xk（t）对应的权重Δwai，j（t）修订为：

（t）可以扩展为如下形式：

其中　

式中：δkj是克罗内可三角数（Kronecker delta）。

同样地，有：

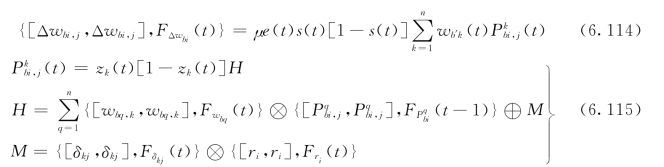
以上递归方程表示非线性动态学习过程，其初始状态为常量，表示如下：