为了显示预测模型的有效性与准确性，将三个模型GM（1，1）、GNNM（1，1）、MNNGM（1，1）分别应用到中国电力需求预测中。根据《中国统计年鉴（1990-2001）》数据，用这三个模型对1990～1998年间的中国电力需求进行预测分析，以对比三个模型的有效性以及三个模型预测精度的不同；同时，根据预测分析的结果对1999～2001年的中国电力需求进行预测，并且与实际观察值进行比较。
为了比较三个模型预测精度的不同，采用了三个不同的误差比较标准，一个是相对误差（RE）；一个是均方误差（MSE）；最后一个是绝对误差（AME）。RE、MSE、AME的公式如下：
式中：x（k）是k时间的实际值；
（k）是k时间的预测值；n是需要预测的数据个数。AME的公式如下：
基于前面对GM（1，1）、GNNM（1，1）、MNNGM（1，1）的分析，根据1990～1998年的历史数据构建三个模型，并进行相对误差分析，计算结果如表6.15所示；同时利用1999～2001年的数据对三个模型进行检验，比较他们的相对误差，具体计算数据如表6.16所示。
表6.15 三个不同的方法对1990～1998年间中国电力需求预测分析
续表
表6.16 1999～2001年预测值
(www.xing528.com)
从表6.15可以看出，三种模型都取得了比较满意的预测效果。通过比较其相对误差可以发现，GNNM（1，1）比GM（1，1）的预测相对误差小，这主要是因为采用了BP神经网络后提高了网络的收敛速率，从而对数据有了比较精确的预测；同时，MNNGM（1，1）比GNNM（1，1）的预测精度也要高。
图6.28、图6.29、图6.30分别给出了三种模型的预测曲线。从图6.28可以看出，虽然GM（1，1）在1990～1996年的预测值比较准确，但1996年后预测的准确性明显下降；从图6.29可以看出，GNNM（1，1）的预测曲线比GM（1，1）的曲线更靠近观察曲线，特别是1998年后的预测值比GM（1，1）更准确；从图6.30可以看出，MNNGM（1，1）的曲线最靠近观察曲线，拥有最高的预测精度。同时，表6.17比较了三种模型的MSE与AME值。
从表6.17可以看出，按照不同的误差标准，MNNGM（1，1）比其他两种算法预测的精度都高。以1999～2001的预测值来分析，MNNGM（1，1）的AME值大约是GNNM（1，1）的2/5，GNNM（1，1）的AME值大约是GM（1，1）的1/2。换句话说，MNNGM（1，1）的预测精度大约是GNNM（1，1）的2.5倍，大约是GM（1，1）的5倍；而从MSE值来看，MNNGM（1，1）的MSE值大约是GNNM（1，1）的1/4，GNNM（1，1）的MSE值大约是GM（1，1）的2/5。由此而见MNNGM（1，1）算法的有效性与准确性。
图6.28 GM（1，1）预测结果
表6.17 不同模型预测误差分析（Mk Wh）
图6.29 GNNM（1，1）预测结果
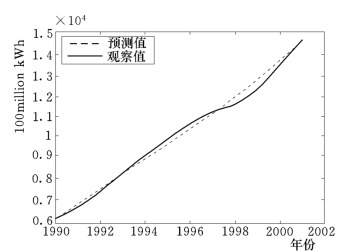
图6.30 MNNGM（1，1）预测结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
