基于灰色神经网络的风险传递预测模型

（1）用BP神经网络对GM（1，1）进行改进，建立GNNM（1，1）模型。为了表述上的方便，把灰色理论中的符号表示改变一下，原始数列x（0）（t）表示为x（t），一次累加生成后得到的数列x（1）（t）表示为y（t），预测所得到的值表示为z（t），这里t∈（0，N-1）。

定理6.3　灰微分方程的解即为时间响应模型。

证明：在灰色系统中，灰微分方程GM（1，1）可以表示为：

根据前面的表述，式（6.75）可以表示为如下形式：

式中：a、u为待定参数。

时间响应模型为：

离散响应模型为：

对灰微分方程式（6.76）进行求解可得如下表达式：

当t＝0时，y（0）＝X（0），则有C＝y（0）-，那么式（6.79）的解为：

从而，证明了对于GM（1，1），其灰微分方程的解即为时间响应模型。同理，对GM（1，N）进行推导也可得到同样结论。

根据以上结论，利用时间响应模型神经网络建模显得更为合理。以下对式（6.77）进行变换，使其映射到一个BP神经网络中，然后对这个BP神经网络进行训练，当网络收敛时，从训练后的BP网络中提取出相应的方程系数，从而得到一个白化的微分方程，进而可利用此方程对系统进行深层次研究或对其进行求解。

对式（6.77）进行如下变换：

将式（6.77）映射到BP神经网络中，其结构如图6.27所示。相应的BP网络权值可进行如下赋值：

y1的阈值设为：

BP神经网络L2层神经元的激活函数取为Sigmoid型函数：f（x）＝。其他层神经元的激活函数取为线性函数f（x）＝x。通过神经网络不断训练，使权值不断修正，这样相当于对灰色参数白化的不断求精，从而使预测的精度增强。基于此，建立了灰色神经网络模型GNNM（1，1）。(www.xing528.com)

图6.27　映射出的BP神经网络结构

（2）GNNM（1，1）的学习算法。

由于灰色BP网络存在与传统BP网络不同的特点，因而要对传统BP网络的学习算法进行改造，以使其适应灰色BP网络。在对灰色BP网络进行训练时要注意两点：一方面，由于w21＝-y（0），所以在BP网络训练过程中，权值w21始终保持不变；另一方面，w31、w32直接由输入与w11得到。具体的学习算法如下：

第1步　根据系统数据列特征，选取两个较小的值作为a、u。

第2步　根据网络权值定义计算w11、w21、w22、w31、w32。

第3步　对每一模式[t，y（t）] （t＝1，2，3，…，N），进行如下操作：

1）将t值输入L 1层节点，并对L2、L3、L4层的节点进行以下计算：

L2层：

L3层：c1＝bw21，c2＝aw22

L4层：d＝w31c1+w32c2

2）计算网络输出与期望输出之间的误差。

由于L 4层激活函数f（x）＝x，因此f′（x）＝1，则L4层误差为：

将误差反向传递到L 3层，L 3层激活函数f（x）＝x，则L 3层误差为：

将L3层误差反向传递到L2层，由于L2层激活函数f（x）＝，则L 2层误差为：

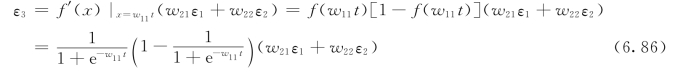
3）调整L2到L3的连接权值。

4）调整L1到L2的连接权值。

5）调整阈值。由于b＝2u/a、w22＝b，故可得到L4层单元阈值的调整式：

第4步　重复第3步，直到误差变为零或达到所需要求。