风险神经网络：一种新型的神经网络模型

图6.18　工序误差变化曲线

人工神经网络的研究从提出到现在已经走过了60多年的道路，在发展的过程中，人们提出了几十种较有影响力的神经网络模型。如：Perceptron（感知机）、Grossberg的自适应理论、Fukushima的神经认知网络理论、Kohonen的自组织映射网络、Hopfield的反馈网络模型、多层BP网络、Boltzmann机、径向基函数网络（RBF）等。经过多年的实践和发展，人工神经网络已经成功应用于模式识别、自动控制、优化计算等领域。

广义项目风险元传递理论的提出，旨在从传递的角度对风险元进行研究，通过分析风险元的传递特征，得到总目标和主要风险元的关系，从而对风险进行有效预测、合理规避，使目标得以优化。本节将神经网络模型和风险元传递理论结合，提出一种新的神经网络模型——风险神经网络。首先，对风险神经网络模型进行一系列定义，提出风险神经元模型的基本函数构成；其次，提出两种典型的风险神经网络的传递模型，分别是前馈风险神经网络模型和多隐层神经网络模型，给出相应的网络输入输出间的映射关系表达式；最后，将模型应用于组合优化问题，结果验证了该算法的有效性。

1.模型基本定义

风险神经元主要由解析、加权、聚合三部分运算组成，分别用符合Θ、⊕、⊗表示。以下分别对这三个算子进行定义。

定义6.17（算子Θ）　解释为对随机变量进行求特征函数，期望E（x）、方差V（x）、偏度S（x）。用Θ1代表求期望，Θ2代表求方差，Θ3代表求偏度。具体定义为：

定义6.18（算子⊕）　解释为加权求和，用来计算风险神经网络的隐层的特征函数，如E（x）⊕w（x）可以定义为：

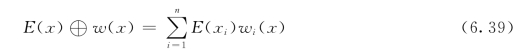
定义6.19（算子⊗）　可以取各种形式的运算，如求和、max、min等，用来进行聚合基函数的运算。

与传统神经元相比，风险神经网络有四个不同之处。

（1）网络的输入元素x1，x2，…，xn都是相互独立的随机变量。

（2）从输入层到隐层需要进行解析运算，求出各个变量的期望、方差和偏度。

（3）网络的隐层由随机变量的特征函数E（x）、V（x）、S（x）表示，隐层的权值为变量x的函数。

（4）在网络中引入聚合基函数G（·），用来进行聚合操作。本网络中取聚合基函数为高斯核函数。

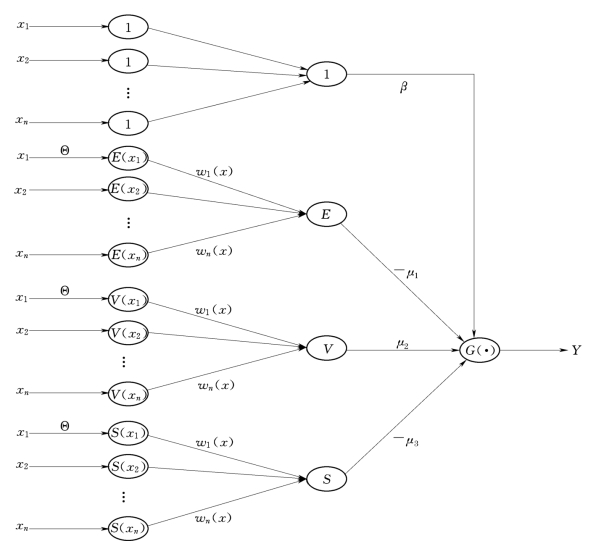
图6.19　风险神经网络模型

如图6.19所示是风险神经网络的模型。其中：x1，x2，…，xn是相互独立的随机变量，其分布函数可以是离散型，也可为连续型；E（xi）为xi随机变量对应的期望；V（xi）为xi随机变量对应的方差；S（xi）为xi随机变量对应的偏度；wi（x）为xi变量对应的权重函数；E、V、S分别代表总期望、总方差、总偏度；μ1、μ2、μ3分别代表风险偏好因子；G（·）称为聚合基函数，可以取很多函数，如sgn函数、Sigmoid函数、高斯函数；β为Lagrange因子。那么输出函数y可抽象定义为：

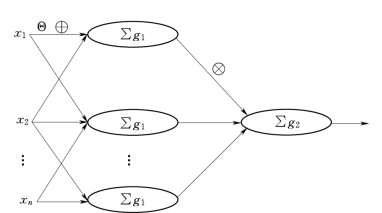
图6.20　前馈风险神经网络模型

2.前馈与多隐层风险神经网络模型

（1）前馈风险神经网络模型。为了使模型得到简化，这里只考虑仅含一个风险神经元的隐层的多输入单输出系统，对于多输入多输出的情况较易得到。取聚合运算⊗为加权和，网络拓扑结构如图6.20所示。

可以得到网络输入输出间的映射关系为：

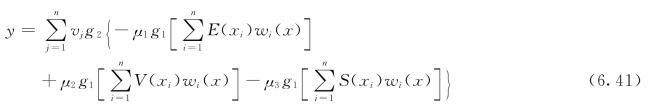
式中：vj为隐层节点j到输出节点i的连接权值；g1为风险神经元聚合基函数；g2为输出节点聚合基函数，g1、g2为非线性函数。

（2）多隐层风险神经网络模型。为提高网络对于系统输入输出之间复杂关系的映射能力和适应性，增强网络的柔韧性和知识存储能力，这里考虑包含多个隐层的风险神经网络模型，设多隐层风险神经网络为一个多输入单输出系统。图6.21所示是双隐层风险神经网络模型，由此可以推广到多隐层风险神经网络。

图6.21　多隐层风险神经网络

可以得到网络输入输出之间的映射关系为：

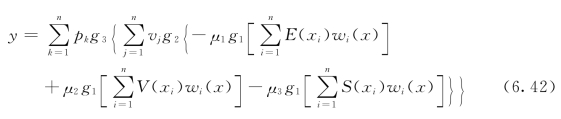
式中：pk为第2隐层到输出层的连接权值；g3为第2隐层的聚合基函数。根据双隐层风险神经网络模型，不难将双隐层风险神经网络模型推广到多隐层模型。多隐层风险神经网络的输入输出映射关系可以描述为：

式中：为第t隐层到输出层的连接值；gt+1为第t隐层的聚合基函数；yt-1为第t-1隐层风险神经网络输出函数；yt为第t隐层风险神经网络输出函数。

3.风险神经网络的传递模型

根据以上对风险神经网络模型的一系列定义，我们将风险元分为离散型和连续型两种情况分别讨论：

（1）风险元为离散型。当x1，x2，…，xn输入为相互独立的离散随机变量，其基本特征函数模型如下：(www.xing528.com)

根据以上对风险神经网络模型的一系列定义，可以将风险元分为离散型和连续型两种情况。

式（6.44）可看做是一个多目标优化问题，通过风险神经网络的传递，使期望和偏度最大化，使方差最小化。根据多目标规划问题的性质，可以将上述多个目标连接在一起，形成求单目标的函数，那么可以将P1转化为一个非线性规划问题，其表达式如下：

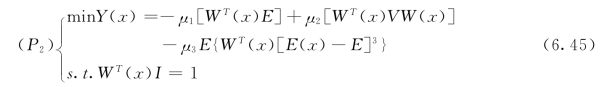
式中：μ1、μ2、μ3是风险偏好因子，分别与E（x）、V（x）、S（x）相关。

对于P2的非线性规划问题的解决一般使用非线性规划技术。也存在一些方法包括目标规划和线性规划方法，被用来解决P2问题，但是整个算法的时间复杂度较高。为了有效地解决P2问题，此处建立风险神经网络的传递模型。

引入Lagrange函数对P2进行变换，可以得到：

式中：β是Lagrange参数。根据Lagrange方程的性质可知，存在β使得W*（x）满足以下的关系：

使用非线性规划理论和系统认知技术，可以证明上述模型可以使用神经学习算法求解，其风险神经网络如下：

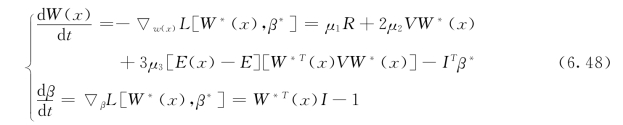
根据6.2.3对风险神经网络的一系列定义，选取聚合基函数为高斯核函数，P2问题可以转化如下：

（2）风险元为连续型。当风险元为连续型分布时，将离散型模型进行变换，可以得到相应的连续风险元的多目标规划模型：

为了使风险神经网络的输出值f（x）最小，和离散型模型处理方式相似，也将P3问题转化为求解非线性规划问题，引入Lagrange函数，对方程的两边求导数，使得满足导数为零的解即为模型的最优解。利用6.2.3对风险神经网络的定义，取目标函数的风险偏好因子，利用神经网络学习，使f（x）最小，从而有效解决了风险神经网络的组合优化问题。

以上的实现过程可以概括如下：

第1步　使用不同的预测模型对项目所存在的风险大小进行预测或对不同项目的同一目标值提出预测。

第2步　根据实际项目的训练规则选取所需要的数据。

第3步　利用概率统计理论，分别得到输入量的期望、方差和偏度。

第4步　利用风险神经网络优化三个目标的组合，得到相应的输出值。

第5步　根据输出值的结果进行决策，对不同的预测模型进行筛选，从而选择较好的优化模型。同时，可以利用RNN对信息进行反馈训练。

第6步　重复第4步到第5步，直至得到最优的输出值。

4.风险神经网络的传递模型应用

为了使模型结果具有对比性，采用参考文献[166]中实例的数据，将风险神经网络应用到投资组合优化问题。根据P1公式中计算期望、方差和偏度的公式，对五个预测模型包括此处提出的RNN模型进行计算，得到如表6.10所示的数据。

表6.10　特征函数的计算结果

同时，选择风险偏好因子分别为（1，2，2）和（2，1，1）计算资产组合的比例，具体数据如表6.11所示。

表6.11　不同的风险偏好因子下，不同的资产所占的比例

表6.12　考虑不同风险偏好因子，各种预测模型下的目标函数的最小值

针对以上的风险偏好因子，可以得到各个预测模型的目标函数的最小值，具体数据如表6.12所示。从表6.12中可以看出，RNN模型的目标值比参考文献[167]中的结果小，说明模型解决组合优化问题具有更好的收敛性。图6.22所示为用Matlab7做的误差分析图，用来比较MLFNN和RNN模型的误差，验证了RNN算法的有效性。

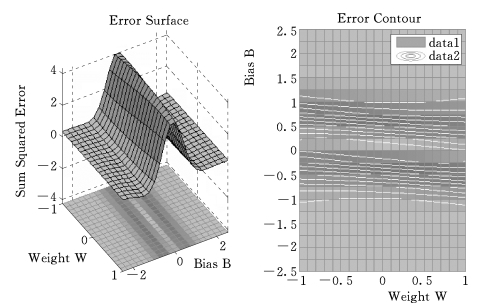
图6.22　误差分析图

表6.10～表6.12中，RW代表随机步行模型，AES代表自适应指数平滑模型，ARIMA代表自回归移动平均模型的集成，MLFNN代表多层前馈神经网络模型，RNN代表风险神经网络模型。