基于神经网络的网络计划风险元传递理论模型优化方案

在工程项目的实施过程中，将受到各种风险因素的影响，这些风险因素会对项目目标的实现产生重要影响。如果在实际项目中对风险估计不足，没有准备有效的风险规避与转移措施，将会对项目的实施与企业的发展带来严重的后果。因此，应该在工程计划阶段，对项目的风险情况有一个全面的认识，估计它的风险程度，在保证工期和费用目标实现的基础上，选择风险程度较小的网络计划路线。

为了有效解决考虑风险因素影响的网络计划问题，本节对网络计划做了重新定义，结合神经网络理论，将经典的网络图转化为基于神经网络的网络图。在此基础上，对工程项目所受风险进行分类，并利用专家评价的方式给出风险在各个工序阶段的评价指标。将该指标作为神经网络的输入向量，设置一定的权值和阈值之后，计算出网络图中各个工序的风险度，进而求出从起点到终点的所有的网络路线的总风险度。最后，用实例验证了本算法的有效性。

1.模型基本定义

为了有效地解决网络计划风险元传递问题，先给出如下基本定义：

定义6.12（经典网络图G）　G＝（V，A，T），其中V＝{v1，v2，…，vn}表示节点集合，A＝{a1，a2，…，am}表示工序集合，T＝{t1，t2，…，tm}表示相应工序上权值的集合。对（vi，vj）∈A赋以权值tij＞0，tij表示从i节点到j节点的工序时间。网络图不能出现回路，两个节点间最多有一个工序。

定义6.13（随机网络）　与经典网络图G不同的是，工序时间tij受风险因素的影响，是随机变化的。

定义6.14（风险元x）　表示随机网络的工序时间，是随机变量，其分布符合概率分布。

定义6.15（风险度δ）　在随机网络中，δi表示ai工序所受各个风险因素经过神经网络综合评价后的风险大小。

定义6.16（基于神经网络的网络图G′）　在随机网络的基础上，定义G′＝（V，A，T，δ），对（vi，vj）∈A赋以权值δ∈（0，1），表示风险度。

由经典网络图转化为基于神经网络的网络图的过程如图6.14～图6.16所示。

图6.14　经典网络图

图6.15　线性神经网络

R—输入向量元素个数；S—第一层的神经元个数；a＝δ＝风险度

图6.16　基于神经网络的网络图

Δij—从i点到j点的神经网络综合评价指数

以风险因素为主要依据，对施工项目风险进行综合评价时考虑的主要因素有：

（1）自然风险。气候条件P1，自然灾害发生情况P2。

（2）经济风险。社会经济状况P3，行业经济状况P4，承包商的经济状况P5。

（3）政治风险。政治环境P6，行业政策变化P7。

（4）技术风险。设计质量P8，设计人员技术P9，施工技术水平P10。

（5）公共关系风险。业主品质P11，监理品质P12，政府部门品质P13。

（6）管理与决策风险。施工部门的管理P14，决策水平P15。

在上述指标体系中，既有定性因素，又有定量因素。因此，对于风险指标P1，P2…，P15，采用专家打分的方法。由于在网络计划中，风险对每个工序的影响大小不同，于是对网络中每一个工序ai所受的风险因素进行专家打分，得出相应工序的风险指标，为计算风险度提供基础。专家打分值为：1.0、0.7、0.5、0.3、0.1五个等级，分别对应风险：高、较高、一般、较低、低。评分时，专家充分审核，根据工程的经验数据和实际情况，给出每个工序各风险指标的评分值，以衡量被评价工序在该指标上的表现，为计算整个工程的风险度奠定基础。

2.基于神经网络的网络计划风险元传递模型

（1）神经网络设计。此处采用神经网络对6.2.2定义的指标体系进行评价。线性神经网络采用线性函数作为传递函数，因此其输出可以取任意值。BP神经网络中的传递函数通常取可微的单调递增函数，如对数Sigmoid函数logsig，正切Sigmoid函数tansig和线性函数purelin。结合广义项目风险元传递理论，给出线性神经网络模型，其他神经网络模型类似。(www.xing528.com)

设网络的输入向量为P＝（P1，P2，…，P15），Pi表示第i个风险指标值；W为神经网络的权值；b为神经网络的阈值；δ为神经网络的输出值，即为风险度。那么，本节的线性神经网络模型可描述为：

由于在实际项目中，当预测到整个网络的风险度较大或在风险度较低但工序的工期或费用不符合要求时，需要调整神经网络的权值和阈值，重新计算风险度，于是将神经网络的权值之和认为是施工网络的费用，将阈值认为是施工网络的工期，这样调整权值和阈值时，也就是在调整网络的费用和工期，既保证了工期和费用满足实际要求，又使工程的风险度达到较低的水平。结合以上定义，基于Widrow-Hoff学习算法的权值和阈值调节原理如下：

其中　

由于　

且有

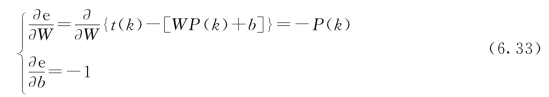
所以，上述权值和阈值的调节公式变为：

即　

式中：η为学习速率，当η较大时，学习速率加快，反之亦然。

在BP神经网络中，权值和阈值的调节规则采用的是误差反向传播算法（BP算法），BP算法实际上是Widrow-Hoff算法在多层前向神经网络中的推广。和Widrow-Hoff算法类似，在BP算法中，网络的权值和阈值通常是沿着网络误差变化的负梯度方向进行调节的，最终使网络误差达到极小值或最小值。

（2）模型算法。下面是基于神经网络的网络计划风险元传递理论模型的具体算法。

第1步　收集相关信息，根据专家判断对每一个工序所受风险进行打分，得到相应的输入向量Pj＝（Pj，1，Pj，2，…，Pj，15），其中，Pj，i表示第i个风险指标的分值。设所有工序的个数为m，那么j＝1，2，…，m。

第2步　根据输入向量Pj＝（Pj，1，Pj，2，…，Pj，15），利用式（6.29）（或者6.2.2节的定义），计算各个工序的风险度δj。

第3步　计算从网络起点到终点的第k条线路的总风险度δk，设总路线个数为n，那么k＝1，2，…，n。其中：，s表示第k条线路上的工序数。

第4步　根据第3步计算的各个线路的总风险度，将风险度从小到大排列，依次检验各风险度对应的路线上的工期和费用是否符合要求。如果最小风险度对应的路线的工期和费用符合要求，那么算法结束。否则，看第二小风险度对应的路线的工期和费用是否符合要求，依次类推，直到找到使工期和费用符合要求的路线。

第5步　根据第4步找到的路线，判断风险度是否在规定的精度之内。如果在，那么算法结束。否则，转入下一步进行神经网络参数调整。

第6步　由6.2.2节的定义，可以通过对权值W和阈值b进行调整，从而计算新的风险度。重复第2步到第5步。

3.网络计划风险元传递模型应用

下面是一工程网络图，如图6.17所示。工程所受风险为6.2.2节中的15个因素，网络图中边上的权值分别为工期范围和费用范围。表6.9是专家对各工序的风险指标评估的数据。评估过程中网络神经元个数S取1；风险元x（ai的工序时间）等于神经网络的阈值b，当工序时间变化时，阈值b相应地调整；ai的工序费用C等于神经网络的权值之和，当工序费用调整时，神经网络的权值相应地调整。

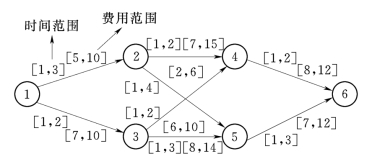
图6.17　受风险影响时的工程网络图

表6.9　各工序的风险评估指标

根据以上数据，利用6.2.2的算法计算各个工序的风险度。采用BP神经网络进行训练，假定目标向量T＝[0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1]，给定的学习精度为ε＝0.001，网络隐含层神经元为3个。分别对这8组数据进行训练，训练次数1000次。那么可以得到图6.18所示的误差变化曲线。

从图6.18可以看出，各工序风险指标经过多次训练后，在规定的精度内达到了目标向量，说明各个工序所受风险度可以达到低水平。根据完工期难易程度评价标准可知，该工程在规定工期和费用内较容易完成。