在项目风险管理中，如何有效、准确地得到费用、工期、风险之间的关系，建立费用—工期曲线，是广义项目风险元传递理论中的重要内容。其中，考虑风险元影响的费用—工期优化问题是项目风险管理的重要方面。目前，国内外对费用—工期优化做了大量研究，传统的方法有CPM法和PERT网络技术。近年来，很多学者将遗传算法（GA）应用其中，取得了很多成果。如参考文献[162]利用GA求解动态网络最佳路径，给出了离散网络最佳路径问题的一般化模型描述；参考文献[163]论述了启发式遗传算法解决最短路径路由优化问题，将可变长度染色体和它的基因应用于编码问题，使算法快速有效。虽然以上文献对费用-工期优化问题从不同角度做了分析，但都没有考虑风险因素的影响，在实际项目管理应用中受到一定限制。
1.GA网络计划风险元传递模型
模型基本假设为：
（1）网络用图论中的图G＝（V，E）来刻画，图中任何两个节点间的边不大于1。
（2）风险元是随机变量，多个风险元是相互独立的，其分布符合概率分布。
（3）各个风险元发生的概率大小或概率分布利用以往相似数据和专家预测的方式来确定。
（4）当风险元概率分布连续时，将风险元表述为各个任务的工期。
数学模型为：引入网络连接的费用矩阵，用C0表示，其中cij为节点i，j（1≤i≤m，1≤j≤n）之间链路的费用。
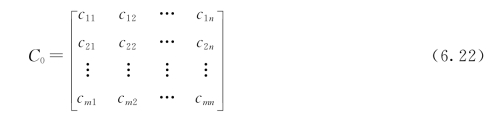
网络计划风险元传递模型的目标为：在考虑风险因素影响的情况下，求出“正常”总工期到“最短”总工期之间所有可行工期的最低费用。相应的数学模型如下：
其中：T0为“正常”总工期；T1为“最短”总工期；θ为网络风险元个数约束常数。
根据机器学习问题的基本模型（见图6.6），受Vapnik等人提出的预测函数模型的启发，在本模型中，使期望风险最小化。
图6.6 机器学习的基本模型
以下建立离散型和连续型两种情况的模型：
（1）风险元为离散型。定义网络链路的风险元矩阵如下：Rk表示第k个风险元矩阵（1≤k≤N），
表示第k个风险元从节点i到节点j之间链路发生的概率（1≤i≤m，1≤j≤n）。
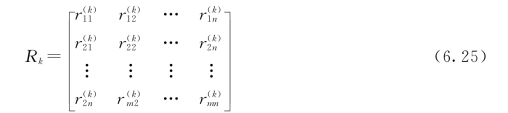
在G＝（V，E）中，可能只有E的一个子集E′受到风险元影响，E′⊆E。全部节点受到第k个风险元影响的概率为
，ni表示第i个节点，P（k）（li）为第k个风险元在第i条链路发生的概率。网络计划风险元模型可描述如下：
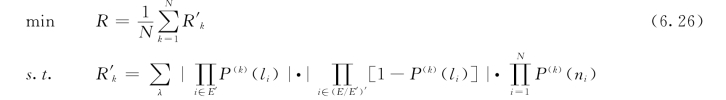
C≤C0
其中：R′k为整个网络所受第k个风险元影响的概率；C0为总费用；λ为网络所有节点受到第k个风险元影响的状态集合；li为第i条链路。
（2）风险元为连续型。对图6.6中的机器学习模型，设F（x，y）为输入x与y之间存在的联合概率，L[y，f（x，y）]为由于用f（x，w）对y进行预测而造成x的损失，称为损失函数。{f（x，w）}称为预测函数集，w∈Ω为函数的广义参数，故{f（x，w）}可表示任何函数集。定义预测的期望风险为：
当给定F（x，y）与L[y，f（x，w）]时，可确定R（w），此处定义损失函数L[p（x，w）]＝-ln p（x，w）。P（x，w）为x的密度函数，同时可将x扩展为x1，x2，…，xN，其中x1，x2，…，xN相互独立。则网络计划风险元模型可描述如下：
2.GA优化网络计划风险元传递模型
遗传算法（GA）是一种基于生物自然选择与遗传机理的随机搜索算法，其实质是由选择—交叉—变异算子组成的周而复始的循环过程。遗传算法在求解复杂优化问题方面具有很大潜力。基本GA的流程如下：编码和初始种群的生成、种群中个体适应度的检测与评估、选择、交叉、变异。
Feng等人在参考文献[164]中采用GA得到了每个可行工期的最低费用，此处参考Feng等人的算法，将风险因素考虑其中，得到考虑风险元的费用优化曲线。
Feng等人提出的算法是一种线性和整数规划模型。模型用到以下概念：费用优化过程曲线，即每一代群体中相应于每一可行工期的最低费用点连线；凸边，即每一代群体中能够从下往上包含所有个体的凸边缘，如图6.7所示。
改进后的具体算法如下：
第1步 编码。编码方式参照参考文献[165]。网络中每个节点对应着不同的风险，每个风险对费用和工期有不同影响。于是，每个节点由数个风险元构成，每个风险元包含三个参数：节点的序号，损失的费用，延长的工期。则同一节点受多个风险元影响时，相应的损失费用和延长工期累加。具体编码构成如图6.8所示。(www.xing528.com)
图6.7 群体凸边与费用优化曲线
图6.8 编码构成
第2步 初始化种群。首先分别得到项目的正常总工期（T0）和最短总工期（T1）。然后，随机产生N-2个个体（N为群体规模）。每一个体代表一种网络计划，个体的值包括由网络计划风险元数学模型求出的总工期以及相应的总的风险值。
第3步 构造适应度函数。首先，确定群体的费用优化过程曲线以及群体的凸边，并计算每一个体到凸边的最短距离（di），如图6.7所示。di在数学上等于个体到凸边每个线段距离的最小值。当考虑风险元影响时，相当于di在坐标平面内发生了坐标平移。图6.9和图6.10所示分别为未考虑风险元的个体适应度计算和考虑风险元的个体适应度计算。其次，确定个体的适应度fi。定义dmax为所有di中最大值，适应度为两者之差。具体的表达形式如下：
fi＝dmax-di
其中 dmax＝max（di） （i＝1，…，N）
图6.9 未考虑风险元的个体适应度计算
图6.10 考虑风险元的个体适应度计算
第4步 选择操作。采用正比于适应度的比例选择机制，其具体操作步骤如下所述。
（1）设群体规模为N，其中个体的适应度为fi，那么任意一个个体被选择的概率为：
（2）计算任意一个个体的累积概率：qi＝
（3）产生一个区间[0，1]内的随机浮点数t，如果t＜q，选择群体中第1个个体，否则选择群体中使qi-1＜t＜qi成立的个体。如此重复N次，产生选择后的N个个体组成配对群体进行交叉、变异运算。
第5步 交叉和变异，产生新一代种群。保留群体中位于费用优化曲线上的个体，并做N-Nno次选择操作（Nno代表优化曲线上个体的个数）。对选择出来的个体按照交叉概率两两进行交叉操作，产生新个体时按照变异概率进行变异操作。通常情况下交叉概率pc∈（0.4～0.99），变异概率pm∈（0.001～0.1）。
第6步 重复第3步到第5步，直到优化过程曲线不再发生变化。
3.基于GA的网络计划风险元传递模型应用
下面是一个网络优化计算的实例，网络如图6.11所示。图6.11中，X（Y）中X代表费用，Y代表工期。
图6.11 实例网络
网络链路的费用矩阵C0和风险元矩阵R0、R1分别如下：
网络节点数N＝6，网络风险元个数约束常数θ＝2，取交叉概率为0.4，变异概率为0.02，遗传操作迭代数为100次，运算结果如图6.12和图6.13所示。
当不考虑风险元影响时，我们得到了如图6.12所示的费用—工期曲线。从图中可以看出，个体的凸边明显向坐标轴靠近，在不同的工期阶段对应于不同的费用。当考虑风险元影响时，如图6.13所示，对应的费用-工期曲线与图6.12相比有远离坐标轴的趋势，这显示了当受风险影响时，工程费用支出增加了，这正好符合实际工程项目。
图6.12 未考虑风险情况下的费用—工期曲线
图6.13 考虑风险情况下的费用—工期曲线
从图中可以看出，经过100次迭代后，凸边上的点明显增多，凸边上的点逐渐形成了曲线。按照工期的不同阶段，形成了分段函数曲线，从而利用该曲线可以近似描述费用-工期曲线。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
