模糊元网络计划风险传递解析模型优化

1.风险元二次划分

在广义项目风险元传递理论模型理论基础中，将风险因素分为两类：一类是这些风险因素的变化，受自然等客观因素的影响，其变化具有随机特性，可用概率和概率分布来描述和表征，这类风险因素称为风险元；另一类是这些风险因素虽然也有变化，但其变化受人为、国家政策等主观因素影响，其变化不具有随机特性，这类风险因素称为敏感元，本书不对敏感元做分析。

考虑到在施工网络计划实际中，存在很多风险元，其中有些风险元的概率和概率分布容易得到，然而另一些风险元的概率和概率分布在实际中很难得到，特别是对一些大型施工项目或者系统而言，如果仅仅从那些容易得到概率和概率分布的风险元出发，对施工网络计划进行分析，建立的模型不能全面反映施工项目，必然导致在实际应用中受阻。因此，需要对风险元进行二次划分，将风险元分为：第Ⅰ类风险元和第Ⅱ类风险元，具体定义如下。

定义6.6（第Ⅰ类风险元）　是广义项目中定义的风险元，在实际的施工项目中，其概率和概率分布容易得到或估计的风险元，属于非模糊随机变量。例如，参考文献[105]建立了水力发电项目经济评价风险元传递解析建模和应用，其概率参数容易得到。

定义6.7（第Ⅱ类风险元即模糊元）　是广义项目中定义的风险元，在实际的施工项目中，其概率和概率分布很难得到或估计的风险元，属于模糊随机变量。

有了上述划分后，可以对广义项目中的施工网络项目进行全面的建模。针对当前施工网络计划研究存在的主要问题，从广义项目的高度对风险元传递模型进行解析，根据GERT网络技术和模糊理论，本书提出了基于第Ⅰ类风险元的GERT网络计划解析模型（6.1.1节已经阐述）和基于模糊元的网络计划完工概率解析模型，以下对模糊元网络计划风险元传递解析模型进行分析。

2.模糊元网络计划的基本定义

定义6.8（模糊元t）　在模糊网络中设工序时间为t，是模糊随机变量，其概率分布在实际中很难求得。

定义6.9（模糊网络完工期Tf）　由从起始节点到终点的时间最长的路径决定。Tf＝max{Ds}，Ds＝。Ds表示从起始节点到终点的通路，Di为工序i的历时模糊数。

定义6.10（完工概率）　指模糊完工期不超过计划完工期的概率，用P来表示，P＝P（Tf≤Tp），其中Tp为计划完工期。

定义6.11（λ-截集理论）　设模糊数为A，μA（x）为模糊事件A的隶属函数，f（x）为概率密度函数，P（A）为模糊事件概率，Aλ为模糊数A的λ-截集，记区间为[aλ，bλ]由μA（x）≥λ确定，那么有：

这样就将模糊事件A的概率转化成了λ-截集Aλ的概率。

3.模糊元网络计划的解析模型及其应用

通过分析模糊元和隶属函数间的变化关系，可以得到模糊元网络计划的完工概率，从而可以动态地分析模糊元和完工概率的关系，当完工概率变化时，对总工期也会产生动态的变化，从而可以进行风险分析。

根据前面对模糊元的定义，利用式（6.17）可以将模糊事件概率转化为λ-截集Aλ的概率。然而，模糊元的概率密度函数不容易得到，这就使模型应用受到限制。参考文献[161]假定概率分布为均匀分布，得到了相应的解析解，给出了模型的灵敏度分析算法，提高了模型的实际应用范围。

根据参考文献[161]，取λ-截集Tfλ为一区间数[aλ，bλ]，由模糊集合截集的性质得，在Tfλ＝[aλ，bλ]区间内，模糊元是服从均匀分布的随机变量，那么概率密度函数为：

设λ∈[0，1]，Tf为计算工期，隶属函数为μ（x），设模糊均值为s，Pλ为随机数取λ时计划工期Tp大于[aλ，bλ]内均匀分布的计算工期的概率，则模糊元网络计划完工概率为：

其中　

图6.5所示为完工概率示意图。

基于以上定义，可以得到：

当Tp＜s时

(www.xing528.com)

图6.5　模糊元网络计划完工概率计算

当Tp≥s时

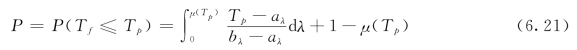
可以从以下步骤进行灵敏度分析：

第1步　当确定的初步完工概率P很高，也就是说风险很低，并且计划完工期Tp令人满意，这时无须进行灵敏度分析，转至第5步；否则，转入第2步。

第2步　当完工概率的风险不令人满意，这时需调整模糊工期，也就是对aλ、bλ、s、Tp做灵敏度分析。

第3步　通过解析方法得到完工概率解析式，对aλ、bλ、s、Tp中的一个或多个进行变化，如在bλ、s、Tp不变的情况下，给aλ加一个Δλ，要使完工概率在0.8～1之间变化，必然可以通过上面的解析方法求出Δλ的范围，算出Δλ就可以分析完工概率的风险。

第4步　当完工概率调整为低风险状态时，还要考虑此时总目标（总工期）是否符合工程实际要求，如果不符合，则返回第3步，再次进行灵敏度分析。

第5步　得到相对满意的结果，算法结束。

这样得到了模糊元网络计划完工概率的解析解，通过给定的模糊工期和隶属函数得到aλ、bλ、s，从而求出完工概率P。在风险分析时，可以通过专家咨询或者根据以往对工程风险的判断，得到对风险的初步划分，表6.8给出了完工概率与工程完工期难易程度评价的关系。

表6.8　完工概率与工程完工期难易程度评价关系

模型应用：

某混凝土双曲拱坝，根据工程施工可行性研究报告和相关施工技术标准及规范，构造了工程大坝施工进度网络计划图，采用模糊元网络计划模型对该工程进行计算分析，可得模糊工期：最小模糊估计62.5天，最大模糊估计90天，平均模糊估计80.5天。设计划完工期为85天，根据以上的算法可以得到：

当t＜s时

当t≥s时

其中，s为模糊均值，s＝80.5。同时可以得到：

aλ＝62.5+18λ，bλ＝90-9.5λ

由于μ（85）＝1-＝0.526，根据式（6.21）可以得到完工概率为：

那么，根据表6.8可知，该工程完工概率在0.85～0.95之间，容易在计划完工期内完成。