风险元传递模型：区间数或模糊数网络型

1.区间数或模糊数网络型风险元传递模型

在缺乏客观数据或数据不足的情况下，很难得到实际问题中树叶节点风险元的概率分布，因此，在有些情况下难以用概率定量方式进行树型风险元传递算法的评价。并且利用概率论研究不确定性的计划网络关键路径问题需要首先假设各活动时间的分布情况，因此，对于缺乏充足先验数据，无法判断各活动时间分布的情况时难以适用。在这种情况下，可以采用模糊数表示不确定活动时间。Shih-Pin Chen对模糊数网络下的关键路径问题进行了研究，这种方法的优点是用人类的主观判断代替未知的先验分布，并不需要任何的先验信息。其根本思想是将模糊数转化成一系列关于α截集上的区间数进行研究，因此可以说研究模糊数的一种基本思路是研究区间数情况下的关键路径问题。

参考文献[159]给出了区间关键路径（Interval Critical Path，简称ICP）的定义、相关定理以及求解方法。然而由于该文对ICP的定义过于宽泛，以至于在通常情况下区间数计划网络可能存在较多的ICP，到底哪一条关键路径该重点控制该文并没有给出相应的讨论。刘春林[160]研究了基于限制期下的区间数关键路径解法，虽然给出了应该重点控制的关键路径，但是添加了限制期这样的一条约束。本节将给出一种基于线性规划问题下的区间数风险元网络关键路径的更一般的算法，并通过实例证明此方法可以提供更准确的工期控制信息，并且计算更加简便。

用确定性线性规划（LP）的方法求解网络中关键路径算式如式（6.10）所示。

网络的具体定义如下：G（V，A）表示一个有向、无回路的计划网络，其中V表示网络中的节点集，A⊂V×V表示连接节点之间的有向弧。用tij表示节点vi到节点vj所经历的时间值，L＝{li|i＝1，…，s}为网络中由起点v1到vn所有路径的集合，D＝{di|i＝1，…，s}表示集合L中相应路径经历的时间的集合。当lk∈L且dk＝max（D）时，称lk为网络G中的一条关键路径。目标函数D（t）表示求网络中起点v1到vn所经历的最大时间，约束条件代表的是流守恒，即除起始节点和终止节点外，进入某一节点的流入和流出值相等，起始节点的流出路径之和为1，终止节点的流入路径之和为1。每个流入或流出变量xij只能取0或1，则关键路径就是满足式（6.3）的解集。

根据6.1.2节所述，当将网络中从起点v1到vn某一条路径li经历的时间di看作一个结果集时，则这条路径上由前至后的依次两个节点之间的活动时间tij（j＝i+1，i＝1，…，n-1）构成了di的一个划分。因此，计划网络可以看成是从起点v1到vn的s条路径用网状图形表示的集合。当考虑不确定性因素且用区间数表示两个节点之间的不确定性时，就构成了区间数的网络风险元计划图。

因此，区间数关键路径的定义如下：

定义6.5　G（V，A）中的路径l∈L是区间数关键路径（Interval Critical Path，简称ICP）的条件是：当且仅当存在一系列实数（i，j∈A），当用tij替代区间数Tij时，l是关键路径。

研究区间数网络风险元计划图需要解决以下两个问题。

（1）区间数计划网络总工期的持续时间。根据式（6.10），可以得到网络风险元计划图的LP求解算式如式（6.11）所示。

式中：，表示区间数。

由于各节点间的时间是区间数的形式，因此根据区间数的运算法则，总工期持续时间也是区间数的形式，假设用表示，则所求问题可以分解为求T（D）和（D）两个问题。

定理6.1　总工期持续时间的左端点（D）等于网络中所有路径中节点间的时间值取左端点时得到路径所经历的时间值，且求得的路径是一条区间数关键路径。即：

证明：由定义6.5易知，由式（6.10）求解后所对应的路径是区间数关键路径，假设求解后路径为l且其持续时间为d，替换网络中各节点的时间形成新的网络，假设重新求解后所对应的关键路径为l′且其持续时间为d′，则有：若l′＝l，由于；若l′≠l，由于l′是关键路径，由6.1.2节可知d′≥d′l≥d，因此定理6.1得证。同理可得到定理6.2。

定理6.2　总工期持续时间的右端点值（D）等于网络中所有路径中节点间的时间值取右端点时得到路径所经历的时间值，且求得的路径是一条区间数关键路径。即：

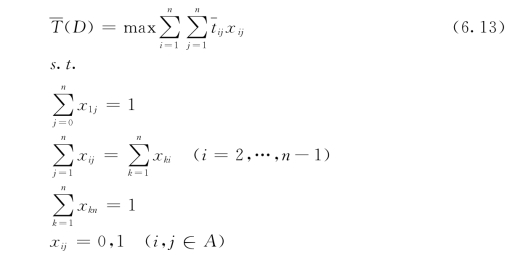
（2）区间数计划网络的关键路径。按照定义6.5，区间数的网络中有可能存在着许多条关键路径。因此，如何在这许多条关键路径中选择最关键的一条路径成为区间数关键路径所要研究的问题。在解决不确定问题的时候，往往需要在工程控制的许多可能产生的结果中选择一种，即在不确定的结果中依照某种准则得出某种决策控制方案。借鉴6.1.2节中的思路，在此定义一个偏好因子λ用来描述选择的偏好。定义偏好函数如下：

因此，结合偏好函数后，最可能关键路径的问题描述如下：

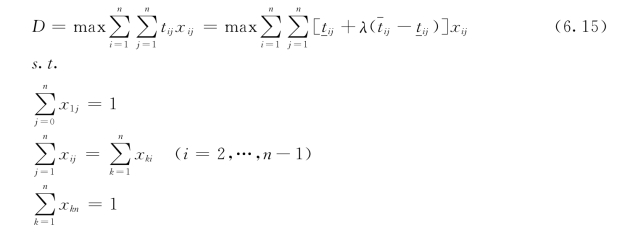
xij＝0，1 （i，j∈A）

从式（6.15）可以看出，求总工期的持续时间的左右端点可以归结为λ＝0和λ＝1时式（6.15）的特解。特别地，当λ＝0.5时，取的是各区间数的均值，相对应的是传统概率下依照期望进行选择关键路径的选择方法。

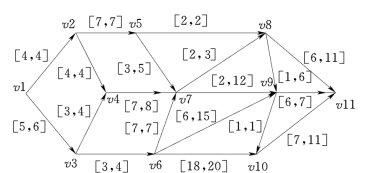
图6.4　某工程控制中的11个节点的计划网络

2.区间数或模糊数网络型风险元传递模型应用

假设某工程的计划网络图如图6.4所示。

根据式（6.15）建立求解方程如式（6.16）所示。

s.t.

x12+x13＝1(www.xing528.com)

x12＝x24+x25

x13＝x34+x36

x24+x34＝x47

x25＝x57+x58

x36＝x67+x610+x69

x47+x57+x67＝x78+x79

x58+x78＝x89+x811

x69+x79+x89＝x911+x910

x610+x910＝x1011

x811+x911+x1011＝1

x12，x13，x24，x25，x34，x36，x47，x57，x58，x67，

x78，x79，x69，x610，x89，x910，x811，x911，x1011＝0，1

用Lingo求得结果如表6.4（取λ步长为0.1，λ∈[0，1]）所示。

表6.4　不同λ值下的关键路径

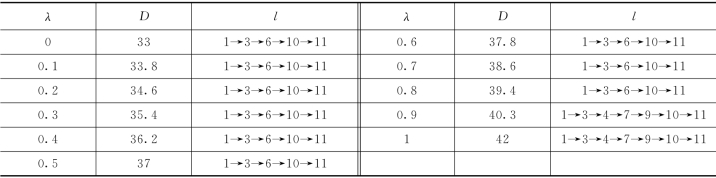
从表6.4可以看出，整个工程的最短完成时间分布范围为T（D）＝[33，42]。并且根据λ的取值不同，有两条关键路径：λ＝0，0.1，0.2，…，0.8，l1＝{1→3→6→10→11}；λ＝0.9，1，l2＝{1→3→4→7→9→10→11}。

将结果所得的两条关键路径代回到目标函数中可得：

D1＝（5+λ）+（3+λ）+（18+2λ）+（7+4λ）＝33+8λ

D2＝（5+λ）+（3+λ）+（7+λ）+（2+10λ）+1+（7+4λ）＝25+17λ

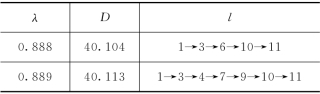
令D1＝D2，得λ＝8/9≈0.8889，即λ＝8/9是关键路径的变化点。对此点用Lingo进行验证，表明结果正确，验证结果见表6.5。

可以看出，偏好因子λ表示的是项目工期变化的关键因素。为了寻找控制子路的优先顺序，定义风险敏感系数δ＝，有δ1＝8，δ2＝17。D2的风险敏感系数较D1大，表明D2有更多的控制时间可供控制。从D2的各子路径λ的系数上看，v7→v9的λ系数最大，表明主要控制这两个节点上的时间可以对整个工期进行较为有效的控制；类似地，D1中的v10→v11的λ系数最大，表明控制这两个节点上的时间可以对整个工程的时间进行更有效的控制，可以进一步缩短工期。

表6.5　λ＝8/9是关键路径的一个变化点

本节提出的网络型区间数风险元方法较之传统的概率方法和其他区间数方法研究有显著的优点，具体分析如下所述。

（1）传统概率方法和网络型区间数风险元方法的计算结果比较，见表6.6。

表6.6　传统概率方法和网络型区间数风险元方法的计算结果比较

若按照传统的概率判别方法，将选择期望较高的工作线路为关键路径进行控制。即本实例中选择λ＝0.5的关键路径l1＝{1→3→6→10→11}进行控制，所得工期为[33，41]。

利用网络型区间数风险元方法所得工期为[33，42]，并且除l1＝{1→3→6→10→11}外给出了另一条关键路径l2＝{1→3→4→7→9→10→11}。从结果中可以看出，传统的概率判别方法可能会对项目工期估计过于乐观，从而低估整个项目工期。而网络型区间数风险元方法给出的结果较之传统的概率判别方法可以给出更准确的工期区间估计，而且可以给出更准确的关键路径。

（2）DBICP[159]和网络型区间数风险元方法的比较，比较结果见表6.7。

按照DBICP的方法，当限制在40天内完成时，应该控制的线路为l1＝{1→3→6→10→11}；而当限制在41天内完成时，控制的路径为l2＝{1→3→4→7→9→10→11}。网络型区间数风险元方法也给出了类似的结论：当λ≥8/9，即控制期多于40.113天时，控制路径发生变化，给出的范围更加精确。此外，DBICP方法基于给定的限制期，基于每一个限制期都需要重新计算一次，而网络型区间数风险元方法在得出不同路径的目标函数后只需要计算一次就可得出关键路径的变化条件，即限制期的范围，较之DBICP计算更加简捷。

表6.7　DBICP和网络型区间数风险元方法的计算结果比较