网络计划项目的总工序时间由各个工序时间组成,受风险因素的影响,各个工序的时间变化具有随机性,因此各个工序的时间即为风险元,采用图示评审技术(GERT)网络模型,通过具有线性特性的信号流图理论来计算随机网络中各节点间的传递关系,利用矩母函数基本性质来计算随机网络中各个工序的概率分布数字特征,从而探求随机网络项目总工期等目标值的概率分布解析解。
1.GERT网络模型简介
GERT网络的基本定义如下:GERT是一种随机网络技术,它充分考虑过程的随机性。其网络图由节点、支线、流三个要素组成,记为D=(V,A,C),其中V={v1,v2,…,vn}表示节点的集合,A={a1,a2,…,am}表示支线的集合。一条方向从vi指向vj的支线记为ai=(vi,vj),表示两节点间的有向边。对每一条支线赋以量cij(cij>0),称为支线ai的流。
在GERT网络中,若存在一个节点支线交错序列![]()
![]() ,支线
,支线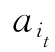 的始点为
的始点为 ,终点为
,终点为![]() ,记为
,记为![]() ,则称这条节点支线交错序列为从
,则称这条节点支线交错序列为从 到
到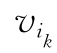 的一条路,记为
的一条路,记为![]() 。若从
。若从 有n(n≥1)条路到达
有n(n≥1)条路到达 ,则记这n条路的集合为总路L={L1,L2,…,Ln},若路的第一点和最后一点相同,则称之为回路。
,则记这n条路的集合为总路L={L1,L2,…,Ln},若路的第一点和最后一点相同,则称之为回路。
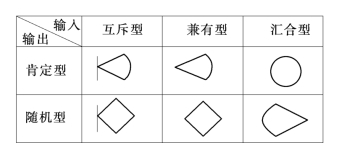
图6.1 GERT网络节点类型构成
以下给出网络中各要素的具体意义:
(1)节点。GERT的节点由输入端和输出端构成,表示一定的逻辑关系。其输入端有三种:互斥型、兼有型、汇合型。输出端有两种:肯定型与随机型。节点类型如图6.1所示。
(2)支线。支线可以表示具体的活动,也可以表示活动的结果,或者两个活动间的相互关系。
(3)流。GERT网络的流主要包含以下三个方面的参数:一条从vi节点指向vj节点的支线实现其所表示工序的概率pij;该支线完成其所表示的工序所需作业时间Tij;该工序时间的概率分布形式fij(t)。
在实际网络计划项目中,受风险因素的影响,要精确得到工序时间的概率分布难度非常大。往往根据实际项目的条件和历史数据对概率分布进行预测。参考文献[157]应用动态随机规划技术对网络完工期进行了计算,利用马尔可夫理论得到的活动工期是指数分布的随机变量,对于符合参考文献[157]假设条件的网络,可以得到工序时间为符合指数分布的随机变量。另外,可以考虑在有历史数据或有专家预测的条件下,利用统计学理论对工序的概率分布作出估计。具体方法如下所述。
引用统计学中的变异系数,对工序的概率分布作出定性的假设,排除一些明显不可能的概率分布。定义变异系数α=![]() ,其估计值为:
,其估计值为:

在实际应用中,当统计了大量数据后它们的期望和方差一般都可以近似求出来,因此可以根据变异系数的定义来对概率分布作出初步判断。例如:对参数为μ、σ的正态分布,V(x)=σ2,E(x)=μ,所以α=σ/μ,如果从实际观测数据中求得α(n)近似等于σ/μ则可初步判断为正态分布,其他分布也可通过变异系数进行估计。
2.GERT网络计划风险元传递解析模型
模型的基本参数定义如下:
定义6.1(风险元x定义) 在GERT网络中,设一条支线ai=(vi,vj)上的工序时间为Tij,定义Tij为这条支线ai对应的风险元xij。其中,xij是随机变量,其分布符合概率分布,设xij的概率密度函数为fij(x)。根据GERT网络的定义可知fij(x)等于工序时间Tij的概率分布形式fij(t)。
由6.1.1的方法可以得到工序时间的初步概率分布,此分布需要在实际项目中进行检验,如果检验为真,那么就可以用来作为风险元的概率分布,如果不真,需要重新进行概率估计或使用新的方法估计。
定义6.2[矩母函数Mx(θ)定义] 设一条支线ai=(vi,vj)对应的风险元为xij,当风险元xij为离散分布时,矩母函数为![]() ;风险元xij为连续分布时,矩母函数为
;风险元xij为连续分布时,矩母函数为![]() 。特别地,当θ=0时,Mx(0)=E(e0)=1必定存在。表6.1给出了常用概率分布的矩母函数。
。特别地,当θ=0时,Mx(0)=E(e0)=1必定存在。表6.1给出了常用概率分布的矩母函数。
表6.1 常用概率分布的矩母函数

定义6.3[特征传递函数wx(θ)定义] 根据GERT网络定义,一条支线ai=(vi,vj)对应工序的实现概率为pij,借助信号流图中的Mason公式,得到一条从vi节点指向vj节点的支线(vi,vj)的特征传递函数为![]() 。
。
定义6.4(风险度λ定义) 风险度λ表示特定节点实现时间(费用)的风险大小。设E(x)、V(x)分别表示风险元的期望和方差,标准差![]() 表示风险的绝对度量,那么风险度λ为:
表示风险的绝对度量,那么风险度λ为:
![]()
对于大部分网络,从结构上可以分为三类:串行结构,并行结构,混合结构。在GERT网络中同样存在这三种结构。这三种结构求解的基本思路是相通的:通过对各个支线上风险元的概率分布的判断,得到相应风险元的概率密度函数,然后得到其各个支线上的矩母函数;利用公式![]() 可以计算出各个支线的特征传递函数
可以计算出各个支线的特征传递函数![]() ,运用信号流图原理根据网络结构求解从一个节点到另一个节点的总路的特征传递函数wE(θ);再利用矩母函数的特征,得到网络中从一个节点到另一个节点的总路的实现概率PE。这样使信号流图和矩母函数在GERT网络中结合起来,实现了对随机网络的求解。
,运用信号流图原理根据网络结构求解从一个节点到另一个节点的总路的特征传递函数wE(θ);再利用矩母函数的特征,得到网络中从一个节点到另一个节点的总路的实现概率PE。这样使信号流图和矩母函数在GERT网络中结合起来,实现了对随机网络的求解。
(1)串行结构。由多个节点连续串在一块的结构称为串行结构。由于具有线性特征,因此可以将许多个串行结构化为一个单向量的等价网络。当从节点vi到节点vz的结构是串行时,那么从vi到vz的传递函数公式为:
![]()
(2)并行结构。并行结构类似于电路理论中的并联结构。设从节点vi到节点vz有n条路,第t条路对应的传递函数为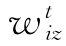 (θ),如果这n条路是并行的,那么这种结构的传递公式为:
(θ),如果这n条路是并行的,那么这种结构的传递公式为:

其中 ![]()

图6.2 混合结构(https://www.xing528.com)
(3)混合结构。在实际GERT网络中,把存在回路的网络结构称为混合结构。基本的混合结构单元如图6.2所示,该结构的传递公式为:

3.GERT网络计划风险元传递解析算法
第1步 构造GERT网络。根据实际项目的基本条件或数据,找到影响项目目标的主要风险因素。
第2步 收集各工序实现概率和工序时间的概率分布的基本参数。
第3步 由Mason公式,根据特征传递函数定义,可得GERT网络中各个支线的特征传递函数![]() ,根据GERT网络的三种基本结构,计算从一个节点到另一个节点的总路的特征传递函数wE(θ)。
,根据GERT网络的三种基本结构,计算从一个节点到另一个节点的总路的特征传递函数wE(θ)。
第4步 设wE(θ)=PEME(θ),其中:PE表示从一个节点到另一个节点的总路的实现概率,在实际中表示工序能否成功实现的概率;ME(θ)为从一个节点到另一个节点的总路的矩母函数。矩母函数性质:当θ=0时,ME(0)=E(e0)=1必定存在。在GERT中引用矩母函数就是为了利用Mason公式计算传递函数,得PE为:
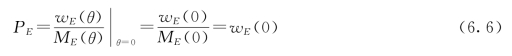
第5步 根据wE(θ)的表达式和PE的值可将风险元传递函数转化为相应的矩母函数,将wE(θ)=PEME(θ)变化可得:

第6步 根据矩母函数性质可得相应从一个节点到另一个节点的总路的风险元期望值和方差的计算公式。

这里的期望表示在风险元影响下,网络中任意两节点工序时间的平均值。有了这个期望,就可以对网络计划项目的实际时间作出比较准确的估计,从而为制订合理的生产安排奠定基础。
这里的方差表示在风险元影响下,网络中任意两节点工序时间的离散程度,离散程度越大,表示风险对工序时间影响越大,反之越小。
第7步 根据式(6.8)和式(6.9),得到风险的绝对度量![]() 和风险度λ=
和风险度λ=![]()
第8步 根据项目风险度的大小,对两节点工序实现时间的风险做出估计,同时可以对关键的工序进行控制。重复第2步到第7步,使网络的时间、费用等参数满足要求。
4.基于GERT网络的风险元传递解析模型应用
为了使模型应用于实际网络计划项目,采用参考文献[158]中所提到的新产品开发项目的GERT网络图。利用表6.2的转化关系将参考文献[158]定义的网络图转化为网络节点,具体网络图如图6.3所示。该产品开发主要包括三个阶段:设计、试验、评估,其中支线2和支线3表示产品设计工作,如果2、3阶段至少有一个工作失败,就转到支线10和支线11进行产品设计工作;支线5和支线6表示产品试验工作,如果需要重新设计则返回3节点;支线8表示产品评估工作,如果评估出产品有问题,需要返回进行设计、试验或评估。图6.3中有两种不同的节点:确定型节点和随机型节点。这两种节点与此处所定义的GERT网络节点的转化关系如表6.2所示。
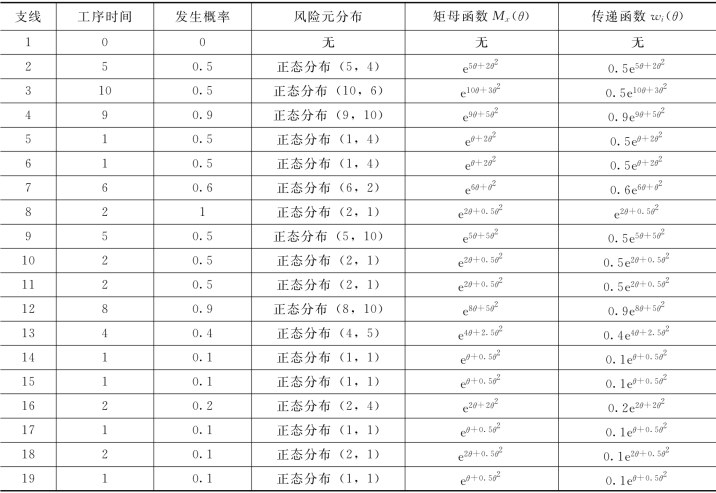
其中,a=1表示互斥型节点,a>1表示兼有型节点。根据表6.2可以将图6.2转化为本章所定义节点类型的GERT网络,如图6.3所示。网络中节点编号、支线编号、工序时间根据参考文献[158]可得。对于确定型节点,其工序时间实现概率为1;对随机型节点,工序时间实现概率根据参考文献[158]所得。参考文献[158]假设了所有支线工序时间的概率分布为正态分布,这样风险元的概率分布也为正态分布,在此基础上,结合6.1.1给出了各支线的正态分布参数,可得到相应风险元的矩母函数和传递函数,具体数据如表6.3所示。
表6.2 参考文献[158]网络节点与GERT网络节点的转化关系

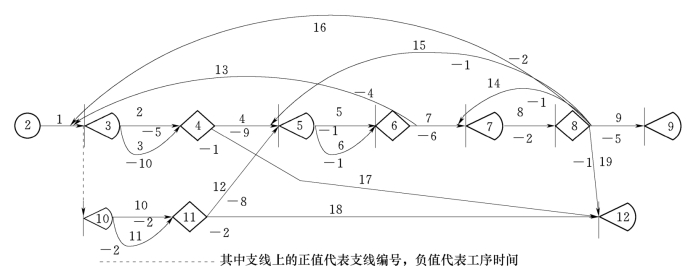
图6.3 GERT网络
表6.3 GERT网络风险元分布参数表
有了以上数据,就可以计算任意两节点间的风险度,下面以计算从节点2到节点7的风险度为例来验证算法的有效性,其他路径可以类似计算。节点2到节点7包括了新产品的设计和试验阶段,由网络图可知,当需要重新设计时,需要从节点6返回到节点10。计算路径的传递函数如下:
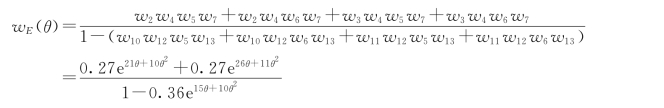
则PE=wE(0)=0.84375。工程完成的矩母函数为:![]() 。利用Matlab7.0计算从节点2到节点7风险元的期望、方差、风险的绝对度量以及风险度如下:
。利用Matlab7.0计算从节点2到节点7风险元的期望、方差、风险的绝对度量以及风险度如下:
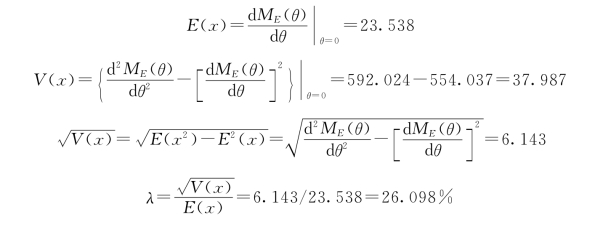
由此可见,虽然从节点2到节点7的实现概率比较大,但风险度也比较大,所以应该严格控制4、6、11节点的工序时间,使设计、试验阶段风险度降低。
对于风险元概率分布的估计是项目管理的难点和重点问题,除了本节所描述的统计方法外,还有其他很多方法可以利用,例如三时估计法、直方图法等,这就需要根据实际项目情况和项目所要求达到的目标进行具体分析。当预知项目总目标的概率分布时,根据本节的解析模型所求得的概率分布特征参数,就可以求得总目标的概率分布,为合理决策提供更加科学的依据。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




