实证分析：企业收益的期望值和均方差概率分布

（1）假设信息不对称风险元x＝1，项目收益期望值为E（ZP）＝2亿元。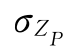＝bx+c中的系数b＝2、c＝2，因此可知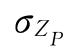＝2x+2＝4。则项目收益的概率密度为：

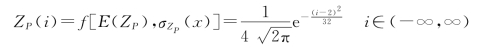
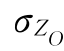（2）企业其他项目收益的期望值为E（ZO）＝10亿元，方差＝dx+g中的系数d＝1、g＝1，因此可知＝1x+1＝2。则由式（5.23）、式（5.24）求得企业收益ZE的期望值和方差分别为：

E（ZE）＝E（ZP）+E（ZO）＝12（亿元）

D（ZE）＝（bx+c）2+（dx+g）2＝（b2+d2）x2+2（bc+dg）x+（c2+g2）＝20

则企业收益均方差　(www.xing528.com)

由企业收益期望值和均方差这两个特征参数即可绘制企业收益的概率密度和概率分布曲线，分别如图5.19和图5.20所示。

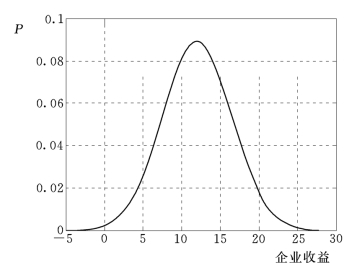
图5.19　企业收益的概率密度曲线

图5.20　企业收益的概率分布曲线

（3）假设企业的借入资金A＝1亿元，银行利率r＝0.05，则企业需在期满偿还本利和A（1+r）＝1×（1+0.05）＝1.05亿元。同时假设银行要求的抵押为B＝0.7亿的固定资产。根据上述企业收入期望值和均方差，采用Matlab软件（详见第7章）即可求得企业收益大于等于1.05亿元的概率为0.9928；小于1.05亿元并大于0.7亿元的概率为0.0014；小于0.7亿元的概率为0.0058；小于0的概率为0.0036。由此可知银行贷款给企业，收回贷款和利息的概率为0.9928，则不能回收本息的概率为0.0072，说明风险很小。