链式风险元传递：定义与解析

实际项目中风险元可以认为由若干个有限状态组成，并且项目的下一状态可以由项目当前所处的状态通过某种关系转移得到，通过每个状态的连续转移直至到达最终目标的过程时，则可以将中间的每个状态看成是风险元，并且此时各风险元的链型传递结构表现为简单的串行传递结构，结合图2.3所示的串行结构，可以构出如图5.12所示的简单风险元传递链。

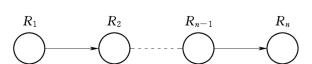
图5.12　一个简单的风险元传递链

为建立基于数据挖掘技术的链型风险元传递理论模型，还需要如下的基本定义。

定义5.1　风险元Ri（i＝1，…，n）是广义项目中的每个状态。其中：R1称为起始风险元，Ri（i＝2，…，n-1）称为传递风险元，Rn表示最终风险元。

定义5.2　在任一风险元Ri中，风险元都会呈现出某种随机状态Xi∈（Q1，Q2，…，Qn），其中X＝{Q1，Q2，…，Qn}称为风险元的状态空间。

定义5.3　风险元的传递过程是由起始风险元R1开始，经历传递风险元Ri（i＝2，…，n-1）最后到达Rn的传递过程。

定义5.4　风险元Ri所处的状态Xi是由前面的风险元开始传递得到的，其概率P（i）表达式如式（5.15）所示。(www.xing528.com)

式中：0≤P（i）≤1。

定义5.5　Ri到Ri+1之间的状态空间概率转移矩阵称为风险元传递矩阵Ai。

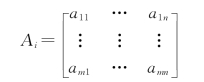
式中：aij表示Ri的状态Qi到Ri+1的状态Qi+1中的转移概率。则Ri和Ri+1之间的传递关系满足式（5.16）。

因此，风险元从R1传递到Rn的传递关系满足式（5.17）。