深度分析事故树定性过程

割集，也称截集或截止集，它是导致顶上事件发生的基本事件的集合。也就是说事故树中一组基本事件的发生，能够造成顶上事件发生，这组基本事件就叫割集。引起顶上事件发生的基本事件的最低限度的集合叫最小割集。

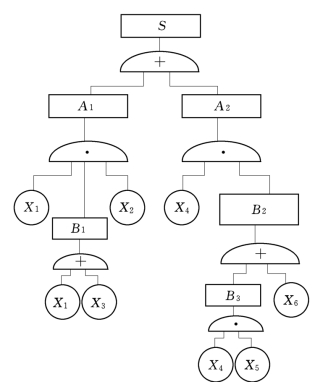
图5.7　事故树结构图

径集，也称通集或导通集，即如果事故树中某些基本事件不发生，顶上事件就不发生。那么，这些基本事件的集合称为径集。不引起顶上事件发生的最低限度的基本事件的集合叫最小径集。

1.最小割集求法

常用的最小割集求法有行列法、结构法和布尔代数化简法[155]，其中以布尔代数化简法最为简单。

行列法是1972年福塞尔提出的方法，所以也称其为福塞尔法。其理论依据：“与门”使割集容量增加，而不增加割集的数量；“或门”使割集的数量增加，而不增加割集的容量。这种方法从顶上事件开始，用下一层事件代替上一层事件，把“与门”连接的事件，按行横向排列；把“或门”连接的事件，按列纵横向摆开。这样，逐层向下，直至各基本事件，列出若干行，最后利用布尔代数化简，得出若干最小割集。

结构法的理论根据：事故树的结构完全可以用最小割集来表示。

布尔代数化简法的理论依据与结构法相似，所不同的只是“∪”与“+”的差别。实质上，布尔代数化简法中的“+”和结构法中的“∪”是一致的。这样，用布尔代数化简法，最后求出的若干事件逻辑积的逻辑和，其中，每个逻辑积就是最小割集。

图5.7所示的事故树用布尔代数化简求最小割集的过程如下所示。

根据布尔代数运算规则，进行计算可得：

S＝A1+A2

＝X1×B1×X2+X4×B2

＝X1×（X1+X3）×X2+X4×（B3+X 6）

＝X1×X1×X2+X1×X3×X2+X4×（X4×X5+X6）

＝X1×X2+X1×X2×X3+X4×X4×X5+X4×X6

＝X1×X2+X1×X2×X3+X4×X5+X4×X6

＝X1×X2+X4×X5+X4×X6（根据A+AB＝A）

所得的三个最小割集为{X1，X2}、{X4，X5}、{X4，X6}。

2.最小径集求法

求最小径集是利用它与最小割集的对偶性。首先作出与事故树对偶的成功树，即把原来事故树的“与门”换成“或门”，“或门”换成“与门”，各类事件“发生”换成“不发生”。然后，求出成功树的最小割集，经对偶变换后就是事故树的最小径集。图5.8给出了两种常用的转换方法。

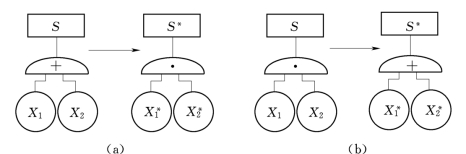
图5.8　事故树结构转换图

（a）“或门”转换为“与门”；（b）“与门”转换为“或门”

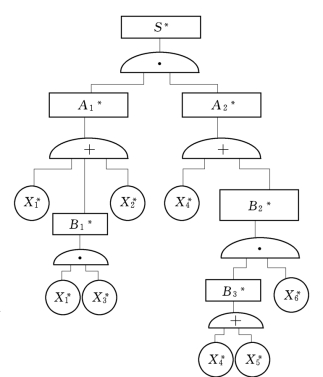
图5.9　与图5.7事故树对偶的成功树

作事故树对偶的成功树时要进行“与门”“或门”转换的原因在于：对于“与门”连接输入事件和输出事件的情况，只要有一个事件不发生，输出事件就可以不发生，所以，在成功树中换用“或门”连接输入事件和输出事件；而对于“或门”连接的输入事件和输出事件的情况，则必须所有输入事件均不发生，输出事件才不发生，所以，在成功树中换用“与门”连接输入事件和输出事件。如图5.8所示，S*、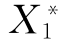、表示事件S、X1、X2不发生。

图5.7所示的事故树对偶的成功树如图5.9所示，图中S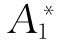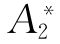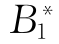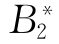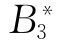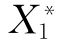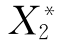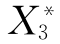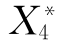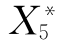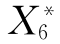*、、、、、、、、、、、分别表示事件S、A1、A2、B1、B2、B3、X1、X2、X3、X4、X5、X6不发生。

用求最小割集的布尔代数化简法，求出最小径集为：(www.xing528.com)

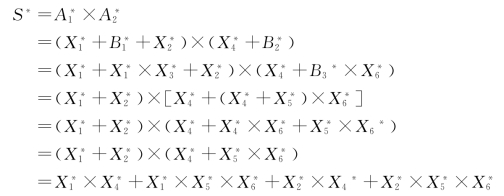
这样，就得到成功树的四个最小割集，经对偶变换得出事故树的四个最小径集，即

S＝（X1+X4）×（X1+X5+X6）×（X2+X4）×（X2+X5+X6）

每一个逻辑和就是一个最小径集，事故树的四个最小径集为：{X1，X4}、{X2，X4}、{X1，X5，X6}、{X2，X5，X6}。

同样，也可以用最小径集表示事故树，如图5.10所示。其中C1，C2，C3，C4分别表示四个最小径集。

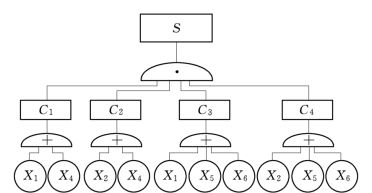
图5.10　最小径集表示的图5.7事故树

3.最小割集和最小径集在事故树分析中的作用

最小割集和最小径集在事故树分析中具有极其重要的作用，其中，尤以最小割集最突出。透彻掌握和灵活运用最小割集和最小径集能使事故树分析达到事半功倍的效果，为有效地控制事故的发生提供重要依据。最小割集和最小径集的主要作用是：

（1）最小割集表示系统的危险性。求出最小割集可以掌握事故发生的各种可能，为事故调查和事故预防提供方便。一起事故的发生，并不都遵循一种固定的模式，如果求出了最小割集，就可以马上知道发生事故的所有可能途径。例如，求得图5.7所示事故树的最小割集为{X1，X2}、{X4，X5}、{X4，X6}，表明造成顶上事件（事故）发生的途径共三种：或者X1、X2同时发生；或者X4、X5同时发生；或者X4、X6同时发生。这对全面掌握事故发生规律，找出隐藏的事故模式是非常有效的，而且对事故的预防工作提供了非常全面的信息。

（2）最小径集表示系统的安全性。求出最小径集可以掌握要使事故不发生的可能方案。例如，图5.10共有四个最小径集：{X1，X4}、{X2，X4}、{X1，X5，X6}、{X2，X5，X6}，表明这四组事件中，任何一组不发生，顶上事件就可以不发生，即只要卡断“与门”下的任何一个最小径集，就可以使顶上事件不发生。

（3）最小割集能直观地、概略地告诉人们，哪种事故模式最危险，哪种稍次，哪种可以忽略。一般来说，一个事件的割集比两个事件的割集容易发生；两个事件的割集比三个事件的割集容易发生……。因为一个事件的割集只要一个事件发生，顶上事件就会发生；而两个事件的割集则必须两个事件同时发生，即满足两个条件才能引起顶上事件发生，这是显而易见的。

（4）利用最小径集可以经济地、有效地选择采用预防事故的方案。从图5.10可以看出，要消除顶上事件S发生的可能性，一般以消除含事件少的最小径集中的基本事件最省事、最经济。消除一个基本事件应比消除两个或多个基本事件要省力。

（5）利用最小割集和最小径集可以直接排出结构重要度顺序。

（6）可以利用最小割集和最小径集计算顶上事件的发生概率和定量分析。

4.结构重要度分析

结构重要度是事故树定性分析中一个重要的重要指标，它表示基本事件对顶事件发生的影响程度。结构重要度分析一般可以采用两种方法，第一种是精确求出结构重要度系数，第二种是用最小割集或用最小径集排出结构重要度顺序。

对于精确求结构重要度系数的方法，可以参照参考文献[154、155]，这里主要说明利用最小割集或最小径集排出结构重要度顺序的方法。需要说明的是，虽然利用第一种方法能精确求出结构重要度系数，但结构重要度分析属于定性分析，只要排出各基本事件的结构重要度顺序即可。

用最小割集或最小径集进行结构重要度分析的基本原则如下所述。

（1）看频率。当最小割集中的基本事件个数不等时，基本事件少的割集中的基本事件比基本事件多的割集中的基本事件结构重要度大。

例如，某事故树的最小割集为：{X1，X2，X3，X4}、{X5，X6}、{X7}、{X8}。从其结构情况看，第三、第四两个最小割集都只有一个基本事件，所以X7和X8的结构重要度最大；其次是X5、X6，因为它们在两个事件的最小割集中；再次是X1、X2、X3、X4，因为它们所在的最小割集中基本事件最多。这样，就可以很快排出各基本事件的结构重要度顺序：

I（7）＝I（8）＞I（5）＝I（6）＞I（1）＝I（2）＝I（3）＝I（4）

（2）看频数。当最小割集中基本事件的个数相等时，重复出现在各最小割集中的基本事件，比只在一个最小割集中出现的基本事件结构重要度大；重复次数多的比重复次数少的结构重要度大。

例如，某事故树有8个最小割集：{X1，X5，X7，X8}、{X1，X6，X7，X8}、{X2，X5，X7，X8}、{X2，X6，X7，X8}、{X3，X5，X7，X8}、{X3，X6，X7，X8}、{X4，X5，X7，X8}、{X4，X6，X7，X8}。在这8个最小割集中，X7和X8均出现过8次；X5和X6均各出现过4次；X1、X2、X3、X4均出现过2次。这样，尽管8个最小割集基本事件个数都相等，但由于各基本事件在其中出现的次数不同，仍可以排出其结构重要度顺序：

I（7）＝I（8）＞I（5）＝I（6）＞I（1）＝I（2）＝I（3）＝I（4）

（3）既看频率又看频数。在基本事件少的最小割集中出现次数少的事件与基本事件多的最小割集中出现次数多的相比较，一般前者大于后者。

例如，某事故树的最小割集为：{X1}、{X2，X3}、{X2，X4}、{X2，X5}，其结构重要度顺序为：

I（1）＞I（2）＞I（3）＝I（4）＝I（5）

上述原则，同样适用于最小径集。按照上述判别原则，可以求出所有基本事件的结构重要度，加以比较后，就能列出相应于结构重要度大小的基本事件的顺序。这个顺序可以反映出各个基本事件在事故树结构中对顶事件发生所造成的影响程度。对于结构重要度大的基本事件，应优先考虑提高它的可靠性，从而降低系统或装置的整体失效概率。