事故树分析就是研究某一个事故树中各基本事件构成的各种集合以及它们之间的逻辑关系，最后达到最优化处理的技术。因此要进行事故树分析，就要对逻辑运算有比较清楚的认识。
逻辑运算的对象是命题。命题分为真命题和假命题，真命题赋值为1，假命题赋值为0，表示对事物规律判断的真假。如1+1＝2就是真命题，赋值为1；1+2＜3就是假命题，赋值为0。
逻辑代数也可进行运算，其基本运算有三种，即逻辑加、逻辑乘、逻辑非。其中逻辑加、逻辑乘用得较普遍。
（1）逻辑加。给定两个命题A、B，对它们进行逻辑运算后构成的新命题为S。若A、B两者有一个成立或同时成立，S就成立，否则S不成立，则这种A、B间的逻辑运算叫做逻辑加，也叫“或”运算。构成的新命题S，叫做A、B的逻辑和，记作A∪B＝S或记作A+B＝S，均读作“A+B”。逻辑加相当于集合运算中的“并集”。
（2）逻辑乘。给定两个命题A、B，对它们进行逻辑运算后构成新的命题P。若A、B同时成立，P就成立，否则P不成立，则这种A、B间的逻辑运算，叫做逻辑乘，也叫“与”运算。构成的新命题P叫做A、B的逻辑积，记作A∩B＝P，或记作A×B＝P，也可记作AB＝P，均读作A乘B。逻辑乘相当于集合运算中的“交集”。
（3）逻辑非。给定一个命题A，对它进行逻辑运算后，构成新的命题为F。若A成立，F就不成立，若A不成立，F就成立，这种对A所进行的逻辑运算，叫做命题A的逻辑非。构成的新命题F叫做命题A的逻辑非，A的逻辑非记作“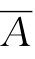
”，读作“A非”。逻辑非相当于集合运算的求“补集”。
此外，逻辑代数运算的法则很多，有的和代数运算法则一致，有的不一致。这里只介绍几种常用的运算法则，以便记忆和运用。
定理5.1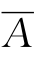 
＝A（对合律）
定理5.2 A+B＝B+A，AB＝BA（交换律）
定理5.3 A+（B+C）＝（A+B）+C，A（BC）＝（AB）C（结合律）
定理5.4 A+BC＝（A+B）（A+C），A（B+C）＝AB+AC（分配律）
定理5.5 A+A＝A，A×A＝A（等幂律）
推论5.1 A+A+…+A＝A，A×A×…×A＝A
定理5.6 A+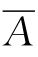
＝1，A×
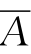＝0
定理5.7 A+0＝A，A×1＝A(www.xing528.com)
定理5.8 A+1＝1，A×0＝0
定理5.9 A+AB＝A，A（A+B）＝A（吸收律）
在事故树分析中“A+AB＝A”，“A+A＝A”和“A×A＝A”几个法则用得较多。
除了需要了解逻辑运算之外，在事故树分析中，还需要了解概率论的基本知识，包括相互独立事件、相互排斥事件、相容事件等[154]，限于篇幅，本书不再赘述。
2.事故树化简
在事故树编制完成之后，为了准确计算顶上事件发生的概率，需要化简事故树，消除多余事件，特别是在事故树的不同位置存在同一基本事件时，必须利用布尔代数进行整理，然后才能计算顶上事件的发生概率，否则就会造成定性分析或定量分析的错误。
图5.5所示的事故树的化简过程如下所示。
由图5.5可知，事故树的结构函数为：
S＝A1+A2＝X1×B1+（X2+B2）＝X1×（X1+X3）+[X2+（X3×X2）]
根据定理5.2及定理5.9，事故树的结构函数可化为：
S＝X1+[X2+（X2×X3）]＝X1+X2
化简后的等效图如图5.6所示。
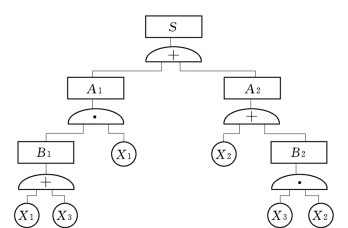
图5.5 事故树结构图
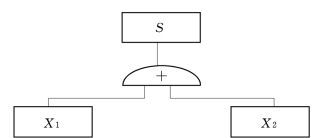
图5.6 事故树等效图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
