区间数或模糊数的树型风险元传递理论及应用

同样地，在缺乏客观数据或数据不足的情况下，很难得到实际项目中树叶节点风险元的概率分布，因此，在有些情况下难以用概率定量方式进行树型风险元传递理论评价。这时，风险元的定量可以采用区间数或模糊数的方式，由于模糊隶属函数可以通过模糊数学中的分解定理或表现定理与区间数进行转换。而在2.8节中曾经给出过模糊数转换成区间数后利用计算机进行风险元传递计算的一个算法，利用该算法和区间数树型结构的风险元传递算法可以实现区间数或模糊数树型结构的风险元传递计算。

仍以图5.2所示的决策树为例对模糊数下的树型风险元传递理论予以说明，所不同的是各风险元的三角模糊数定量方式如表5.3所示，参照2.8节中区间数风险元传递的算法，可以得到决策属性的三角模糊数分布，其计算中间过程如表5.4所示，计算结果如表5.5所示，计算生成的图如图5.3所示（实线代表风险元的模糊分布，虚线代表决策属性的模糊分布）。

表5.3　各风险元的区间数定量形式

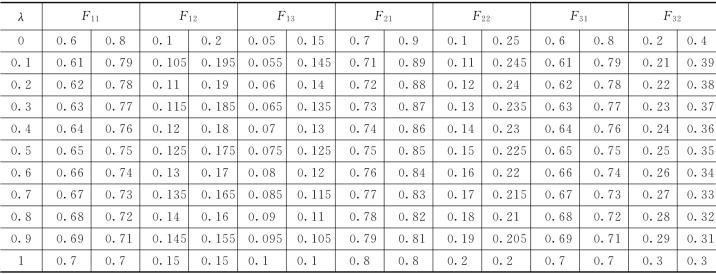
表5.4　各风险元的区间数定量形式

(www.xing528.com)

表5.5　树根节点决策变量模糊数表示结果

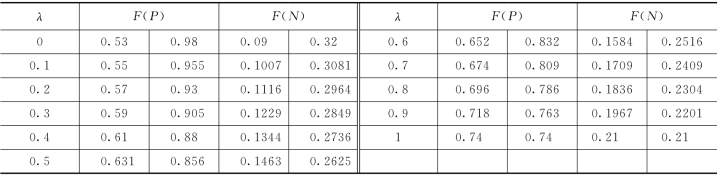
图5.3　风险元（实线）以及所得到的决策变量（虚线）的模糊分布

（a）[60%，75%，80%]；（b）[10%，15%，20%]；（c）[5%，10%，15%]；（d）[70%，80%，90%]；（e）[10%，20%，25%]；（f）[60%，70%，80%]；（g）[20%，30%，40%]；（h）λ＝0时F（P）；（i）λ＝0时F（N）