假设在某工程项目管理中含有表5.1所示的信息集[152]。该信息集表示工程项目的环境因素对工程项目实施结果的影响。
表5.1 示例信息集

续表
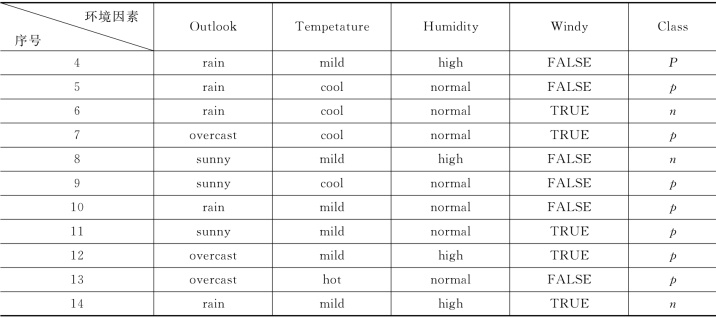
可以将表5.1看成是一个关于工程项目管理中关于自然风险的数据集,属性Outlook、Temperature、Humidity和Windy看成是影响工程项目风险结果Class的风险元,从ID3算法的角度来看,将属性Outlook、Temperature、Humidity和Windy看成是条件属性集C,并且分别以ai(i=1,2,3,4)表示,而属性Class看成是决策属性D。在利用ID3算法之前先对此表用粗糙集理论进行属性约简以简化计算。计算如下:

由式(5.6),有:
POSIND(c)(D)={1,2,3,4,5,6,7,8,9,10,11,12,13,14}=U
考察ai(i=1,2,3,4)在C中相对于D来说是否必要,因此,从C中去掉a1,得到:(https://www.xing528.com)
POSIND(c-{a1})(D)={2,5,9,10,11,13}≠POSIND(c)(D)
可以得出结论a1(Outlook)对于决策属性Class是必要的,不能约简。依次计算可以得到条件属性a2(Temperature)对于决策属性Class是不必要的。这样可以得到核集CORDD(P)={a1,a3,a4}。基于上述计算,在数据挖掘生成决策树算法之前已经去掉了属性a2,简化了计算。

图5.2 经计算后生成的决策树
接下来采用ID3算法生成决策树。利用式(5.2)、式(5.3)和式(5.4)可以得到该信息集的期望信息量为E(C)=0.940286。进而计算Gain(a1)=0.24675;Gain(a3)=0.151836;Gain(a4)=0.048127。选择a1为决策树的根节点,将a1的取值作为从根节点引出的各条分支。然后在各条分支的划分所得的数据子集中继续用式(5.2)、式(5.3)和式(5.4)计算后可以生成如图5.2所示的决策树。
假设各个风险元的分布律如表5.2所示,则根据式(5.1)可以得到如下最终结果的分布律:
f(P)=p12+p11p21+p13p32
f(N)=p11p22+p13p31
表5.2 各风险元的分布律

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




