网络层次分析法在项目社会评价中的风险传递及应用

三角模糊数模糊网络层次分析法的项目社会评价风险元传递理论只适用于评价项目各决策层之间的单向层次关系，而没有考虑不同决策层或同一层次之间的影响，但在实际工作中，常会遇到各因素交叉作用的情况，这时宜采用网络分析法（ANP），为避免对评价指标量化判断时的不确定性与模糊性，将三角模糊数引入网络分析法，形成三角模糊数网络层次分析法的项目社会评价风险元传递理论。

1.建立项目社会评价风险元传递的ANP模型

项目社会评价指标体系是一个复杂系统，有的项目在进行社会评价时其体系中同层指标之间是非独立的，且上下层指标存在相互反馈关系，应用网络分析法（ANP）来构建项目风险等级模型。在本节所举例中，控制层里没有评价准则，网络层里有6个元素集，其中，R1为社会经济风险元，R2为社会环境风险元，R3为生态环境风险元，R4为节约资源风险元，R5为技术开发风险元，R6为项目与社会适应性风险元，这6个元素集是互相依赖的，每一个元素集都存在一个反馈环。

在该模型中，ANP将系统元素划分为两大部分：第一部分称为控制元素层，包括项目目标及决策准则，所有决策准则均被认为是彼此独立的，且只受目标元素支配。控制元素层中可以没有决策准则，但至少有一个目标。控制层次就是一个典型AHP层次结构，所有的准则彼此独立，下一个准则只受上一个准则支配，每个准则的权重均可用传统的AHP法获得。第二部分为网络层，由所受控制层支配的元素组成，元素间相互依存、相互支配，元素和层次间内部不独立，递阶层次结构中的每个准则支配的不是一个简单的内部独立的元素而是一个相互依存、反馈的网络结构。

控制层和网络层组成为ANP模型结构图，如图4.6所示。

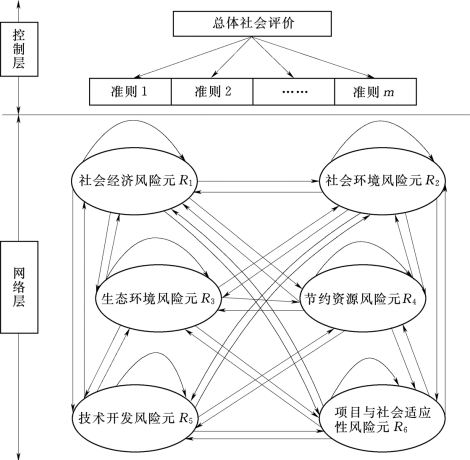
图4.6　项目社会评价风险元传递的ANP模型结构图

其中：表示社会经济风险元R1中的元素与社会环境风险元R2中的元素相互影响；表示社会经济风险元R1中的元素互相影响。

2.项目社会评价风险元传递ANP模型的超矩阵和加权超矩阵

（1）项目社会评价风险元传递ANP模型的超矩阵。AHP的一个重要步骤就是准则间的比较，即在一个准则下，受支配元素进行两两比较，由此获得判断矩阵。但在ANP中被比较元素之间可能不是独立的，而是相互依存的，因而这种比较将以以下两种方式进行。

1）直接优势度。给定一个准则，两元素对于该准则的重要程度进行比较。

2）间接优势度。给出一个准则，两元素在准则下对第三个元素（称为次准则）的影响程度进行比较。

第一种比较适用于元素间互相独立的情形，第二种比较适用于元素间互相依存的情形。

设项目社会评价风险元传递ANP模型的控制层中有元素p1、p2、…、pm，控制层下面的网络层有元素（风险元）R1、R2、R3、R4、R5、R6，其中每个元素下还有下层风险元，其结构如图4.5所示。

以控制层元素ps（s＝1，2，…，m）为准则，在元素集Rj中，以元素Rjl（l＝1，2，…，nj）为次准则，元素组Ri中元素按其对Rjl的影响力大小进行间接优势度比较，即在ps下构造如下判断矩阵。

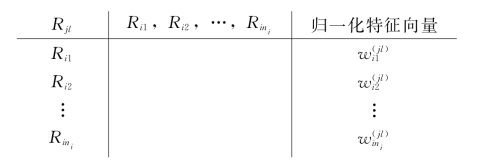
根据一致性检验，如果上述特征向量满足相容性条件，则为元素集Ri中的元素相对于Rjl的重要度排序向量（）′，则得出Wij为：

这里Wij的列向量就是Ri中的元素Ri1、Ri2、…、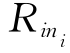对Rj中元素Rj1、Rj2、…、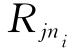的影响程度排序向量。若Rj中元素不受Ri中的元素影响，则Wij＝0。把所有网络层元素的相互影响的排序向量组合起来，即把所有Wij组合起来，得到一个在总体社会评价下的超矩阵，即未加权超矩阵，如式（4.26）所示。

（2）项目社会评价风险元传递的ANP模型的加权超矩阵。当超矩阵的列向量之和为1时，才符合随机原则。未随机化的超矩阵称为未加权超矩阵，将其乘以各群组的权重，则正规化为加权超矩阵，加权矩阵多次相乘之后，将会收敛至一固定值，即此时矩阵的行向量相同，而列向量之和为1，则为极限超矩阵，从极限超矩阵中可得各元素的相对权重。

上述超矩阵的子块Wij是列归一化的，但W却不是列归一化的。为此，在ps下各组元素对准则Rj（j＝1，2，3，4，5，6）的重要性进行比较。

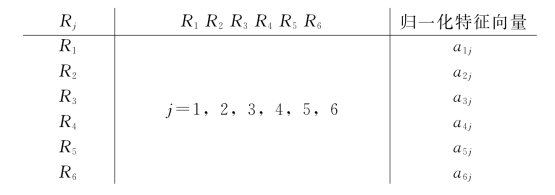
与Rj无关的元素组对应的排序向量分量为零，由此得到加权矩阵R为：

对超矩阵W的元素加权，得：

式中：i＝1、2、3、4、5、6；j＝1、2、3、4、5、6。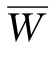即为加权超矩阵，其列和为1，成为列随机矩阵。

在网络分析中加权超矩阵的元素的大小反应元素i对元素j的一步优势度，元素i对元素j的优势度还可以用得到，称为二步优势度，即为的元素，仍然是列归一化的。

当存在时，的第j列就是ps下网络层中各元素对于元素j的极限相对排序向量。的存在性讨论如下：

1）设A为n阶非负矩阵，λmax为其模最大特征值，则有：

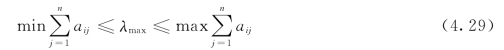
且列随机矩阵的模最大特征根为1。

2）设非负列随机矩阵A的最大特征根为1，是单根，其他特征值的模均小于1，则A∞存在，且A∞的各列都相同，都是A的属于1的归一化特征向量。

当超矩阵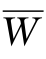满足上述条件时，只要用幂法求出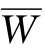的特征值1对应的特征向量v1，则可以得到，其每一列均为极限相对排序向量。

3）非负不可约矩阵A的特征值的和即矩阵的迹为正数时，则A为素阵。

4）设A为n阶非负不可约矩阵，则对任意δ＞0，A+δI为素阵。

由此可知，对内部依存系统的超矩阵，总可用幂法或带有位移的幂法求出。

5）设A为n阶非负不可约矩阵，若对所有1≤i≤n，有aii＞0，则A为素阵，则对每个正整数k，Ak也是素阵。

6）设A为n阶非负不可约矩阵，则对每个1≤i，j≤n存在，正整数k＝k（i，j）使得的元素＞0。

7）设是非负不可约列随机矩阵，则存在的充分必要条件是是素阵。

8）加权超矩阵与平均极限矩阵属于最大特征值1的特征向量相同。

9）当循环系统某一层次内部依存时，其加权超矩阵必为素阵，故存在，且其每一列均为特征值1对应的归一化特征向量。

3.三角模糊数网络分析法的项目社会评价风险元传递理论步骤

（1）根据项目的总体社会评价风险元目标，建立社会评价风险元传递的网络分析法（ANP）模型。(www.xing528.com)

（2）构造用三角模糊数构成的各决策准则间模糊成对比较矩阵，分别计算其权重向量。其中比较标度方法按照表4.13。

（3）构造用三角模糊数构成的决策指标间模糊成对比较矩阵，分别计算其权重向量。其中比较标度方法按照表4.13。

（4）超矩阵的整合与计算。

（5）指标相对重要度权重总排序。

4.应用实例

经过分析研究，在对项目A社会风险元进行评价时，发现项目A中的社会评价风险元是网络结构形式，而不是递阶层次结构形式，即系统中的每个元素可能影响其他元素，系统中每个元素又可能受其他元素的影响和支配，为此建立三角模糊数的网络分析法的项目社会评价风险元模型，重新进行社会风险元评价。评价过程在Matlab环境下编程实现。

（1）建立项目社会风险元评价指标体系的网络分析法（ANP）模型，各决策准则下又包含若干评价指标，共同组成合作决策指标体系，如图4.6所示。为简便起见，在此仍然只考虑社会经济风险元R1、社会环境风险元R2、生态环境风险元R3以及节约资源风险元R4，其中社会环境风险元R2只考虑当地人口风险元、社会安定稳定风险元以及当地人民对项目态度风险元。

（2）采用模糊语意变量尺度来描述各准则间成对比较时的相对重要度，分别以各个评价准则为评估构面，建立决策准则间的模糊成对比较矩阵。

以社会经济风险元R1决策准则为评估结构为例，该评估构面下各准则间成对比较矩阵如表4.17所示，其中比较标度方法按照表4.13。

表4.17　社会经济风险元R1评估构面下各评价准则间模糊成对比较矩阵

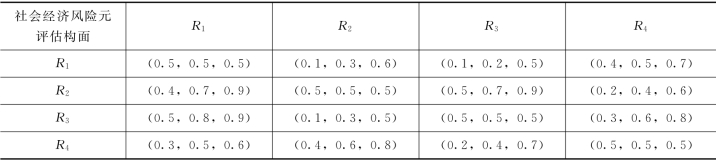
（3）由式（4.11）计算每个准则同其他准则相比较的综合重要程度值。

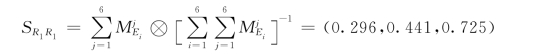
（4）由式（4.12）计算某个三角模糊数大于其他模糊数可能性程度。

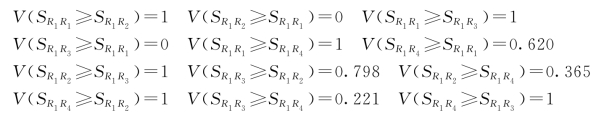
（5）由式（4.13）计算出各评价准则重要于其他准则的可能性程度。

由此，W′R1＝[d′（A1），d′（A2），d′（A3），d′（A4）]T＝（1，0.105，0，0.620）T。

归一化后为：

同理可得到以其他准则为评估构面时各准则的相对重要度为：

将其整合为评价准则间影响权重矩阵，为：

每行（列）分别为R1、R2、R3和R4准则间的影响。

（6）构建评价指标间的模糊成对比较矩阵，构建评价指标群组间元素的模糊成对比较矩阵与构建决策准则间的模糊成对比较矩阵类似。

以资源所在地风险元R42评价指标为评估构面为例，与之关联的群组为社会经济风险元R1群组，该群组内各评价指标间模糊成对比较矩阵见表4.18。

表4.18　资源所在地风险元R42评估构面下各相关评价指标模糊成对比较矩阵

经计算得到：

由此得到：＝（1，0.872，0.691）。

归一化后为：

（7）超矩阵的整合与运算。将各个评价指标模糊成对比较矩阵的权重向量整合在一起便构成了未加权超矩阵，见表4.19，加权超矩阵见表4.20，极限超矩阵见表4.21。

表4.19　未加权超矩阵（×10-3）

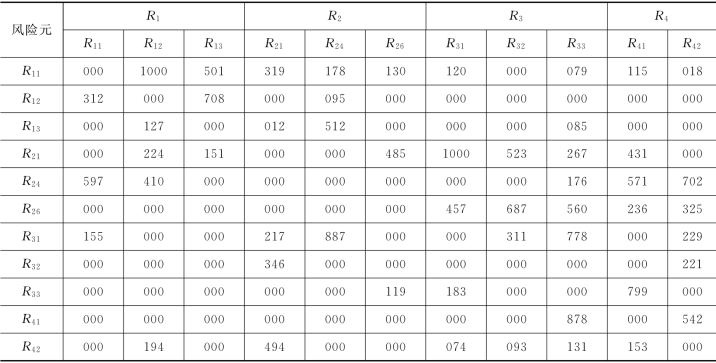
表4.20　加权超矩阵（×10-3）

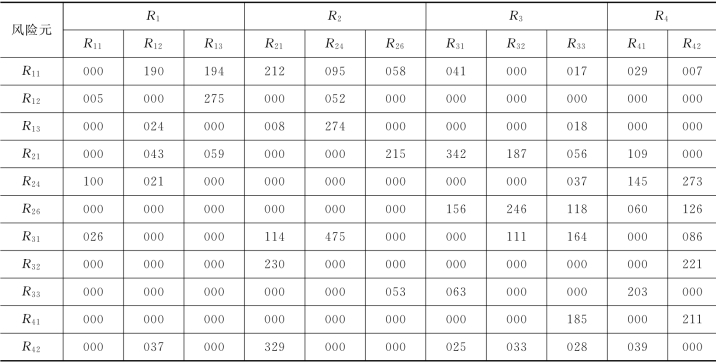
表4.21　极限超矩阵（×10-3）

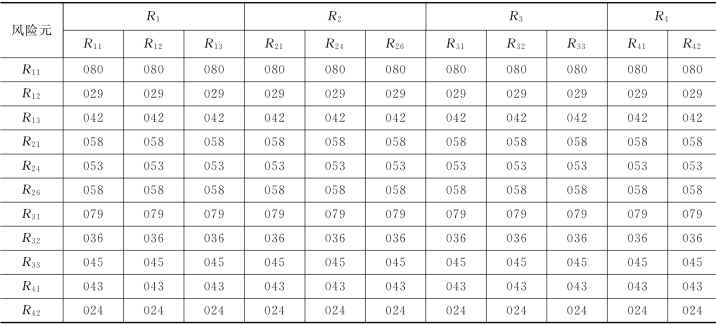
根据以上极限超矩阵的运算结果，决策指标收益分配风险元R11与污染物排放风险元R31的权重系数最高，这是项目进行社会评价风险元的关键性影响因素。

（8）根据各个决策指标的相对权重系数进行综合评分。