模糊数定量方式的层次型风险元传递理论

除上文提到的区间数外，人们发现，对待实际项目中的不确定情况还可以通过语义上的模糊性予以解决，即可以应用模糊数学的知识解决现实中不确定情况的定量问题。因此，有许多学者致力于用模糊数学来拓展层次分析法的适用范围，以期望可以将层次分析法用于解决不确定性问题的决策评估。其中三角模糊数层次分析法（FEAHP）应用最为广泛，用三角模糊数确定权重的步骤如下：

（1）将传统层次分析法中的两两因素比较矩阵中的1～9的数值用三角模糊数的方式代替，相应的代替数值见表4.10。

表4.10　模糊三角数转换表

若一个指标体系中评价指标集可以表示为x＝（x1，x2，…，xn），则使每一个指标xi（i＝1，2，…，n）分别与其他指标进行重要性程度对比，可以给出n个三角模糊数区间分析值，表示为，这里（j＝1，2，…，n）表示三角模糊数，如图4.3所示。

图4.3　模糊三角数（N）

图4.3中，a为隶属于所属论域的最小可能值；b为隶属于所属论域的最可能值；c为隶属于所属论域的最大可能值。对于两两因素比较矩阵，可以用式（4.11）计算第i个目标的模糊综合评价值。

其中　

（2）由式（4.12）计算两两模糊数的可能比较值。

（3）取最小比较值作为最终值，其定义见式（4.13）。

（4）假设d′（Ai）＝min V（Si≥Sk）（k＝1，2，…，n；k≠i），则权重向量可以表示为：W′＝[d′（A1），d′（A2），…，d′（An）]T，然后将其标准化，则可以得到标准后的向量为：

W＝[d（A1），d（A2），…，d（An）]T

由此可以按照FEAHP的方法得到每一层评价指标的权重向量，然后从顶层到底层逐步分配向量权重可得最底层指标的权重向量。

同样，可利用三角模糊数来定量化风险元，将风险元Xi用[min（Xi），P（Xi），max（Xi）]的三角模糊数来表示。其中：min（Xi）表示的是隶属于所属论域的最小可能值；P（Xi）表示的是隶属于所属论域的最可能值；max（Xi）表示隶属于所属论域的最大可能值。结合式（4.4）可以推求总目标特征值的计算公式：

则可以通过计算得到总目标的风险元评价结果[min（S），P（S），max（S）]，然后利用得到的各评价对象的总目标值来进行决策。

以4.2节中的供应商选择实例对上述计算过程予以说明，其过程如下：

（1）确定第二层的权重向量，令第二层的综合值分别为S1、S2、S3、S4，根据式（4.11）计算得：

S1＝（5.67，7，8.5）⊗（1/23.41，1/19.17，1/15.17）＝（0.24，0.37，0.56）

S2＝（3.57，4.5，5.67）⊗（1/23.41，1/19.17，1/15.17）＝（0.15，0.23，0.37）

S3＝（2.74，3.5，4.67）⊗（1/23.41，1/19.17，1/15.17）＝（0.12，0.18，0.31）(www.xing528.com)

S4＝（3.17，4.17，4.57）⊗（1/23.41，1/19.17，1/15.17）＝（0.14，0.22，0.30）

（2）根据式（4.12）比较S1、S2、S3、S4，有：

V（S1≥S2）＝1 V（S1≥S3）＝1 V（S1≥S4）＝1

V（S2≥S1）＝（0.24-0.37）/[（0.23-0.37）-（0.37-0.24）]＝0.48

V（S2≥S3）＝1 V（S2≥S4）＝1 V（S3≥S1）＝0.27 V（S3≥S2）＝0.76

V（S3≥S4）＝0.81 V（S4≥S1）＝0.29 V（S4≥S2）＝0.93 V（S4≥S3）＝1

（3）根据式（4.13）可得：

d′（S1）＝min V（S1≥S2，S3，S4）＝1 d′（S2）＝0.48 d′（S3）＝0.27 d′（S4）＝0.29

（4）得到权重向量W′＝（1，0.48，0.27，0.29）T，将其标准化，可得：

Wc＝（0.49，0.24，0.13，0.14）T

类似地，可得第三层中的各权重向量为：

Wc1＝（0.58，0.30，0.12）TWc2＝（0.41，0.21，0.26，0.12）T

Wc3＝（0.43，0.23，0.29，0.05）TWc4＝（0.61，0.06，0.21，0.12）T

经计算得最终的权向量为：

W＝（0.25，0.13，0.14，0.09，0.04，0.05，0.03，0.05，0.03，0.04，0.01，0.08，0.01，0.03，0.02）T

因此，总目标评价值的计算公式为：

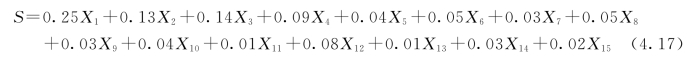
（5）经专家调查得供应商S1和S2的10个风险元的最小值、最可能值和最大值三个模糊特征值如表4.11所示。

表4.11　经调查得到的供应商S1和S2的模糊三角数特征值

（6）用模糊数定量方式层次风险元传递理论，经计算得总目标结果见表4.12和图4.4。

由表4.12可知，S2的三个值均大于S1，从图4.4可以看出，S2的整体位置偏右，即总体来讲S2大于S1。所以一般来说，决策者应选择S2方案作为最优方案。总之，模糊定量方式的层次型风险元传递理论产生的结果和概率定量方式的层次风险元产生的结果类似，都会给决策者提供更多的决策信息。

图4.4　经计算得到的供应商S1和S2的总目标结果

表4.12　经计算得到的供应商S1和S2的总目标结果