区间数层次型风险元传递解析模型优化

由于传统层次分析法中的两两比较矩阵在一般情况下使用1～9进行评分时会使人难以抉择，例如对于1～9中间的偶数数字和奇数数字的差别很少有人能够明确地进行抉择。为此，可以利用区间数代替固定的1～9之间的数值，这时就形成了区间数下的层次分析法（IAHP）。当利用IAHP分析法时，在确定评价指标体系的过程中，一般要对指标进行类型的一致化处理。对于常见的指标而言，一般可分为两种类型，即极大型指标和极小型指标。极大型指标是指属性值越大越好的指标；而极小型指标是指属性值越小越好的指标。此外，还要对指标进行无量纲化处理。在对含有区间数属性值进行综合评价时，需要引进区间数的运算法则对各评价方案的属性向量组成的评价矩阵进行规范化处理。处理方法如下：

设为评价矩阵。其中，m、n分别表示属性个数和评价对象个数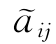，＝[a-，a+]。结合区间数的运算法则，通过式（4.8）、式（4.9）可将A转化为规范矩阵，其中＝[r-，r+]，I1、I2分别表示极大型、极小型指标[142]。

得到规范矩阵之后，需要确定各指标的权重系数，即得到一个权重向量w＝（w1，w2，…，wm）T。得到权重向量之后，可知，评价对象的综合评价值与权重向量和规范矩阵的关系是：z＝w R＝（z1，z2，…，zn）T。值得注意的是：得到的综合评价值也是区间数的形式，要完成综合评价，就要对得到的综合评价值给出排序结果。这时可用区间数的可能度公式进行计算，计算出可能度矩阵P＝（pij）n×n，其中pij＝p（zi≥zj）。然后通过式（4.10）的区间数排序向量公式进行排序：

以下举一个实例对区间数层次型风险元传递理论应用予以说明。假设某电力建设工程项目中有方案集xi（i＝1，…，5）T，各方案结合指标属性以及风险因素后，经调查得到区间数属性值如表4.9所示。

表4.9　某电力建设工程方案的指标属性区间值（亿元）

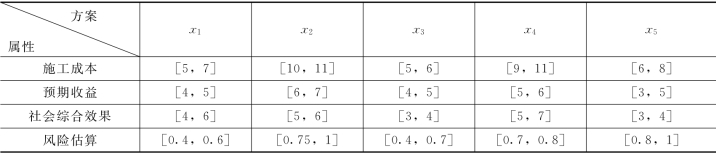
其中：施工成本和风险估算属于极小型指标，预期收益和社会综合效果属于极大型指标。

（1）给出评价矩阵A＝（）4×5。

（2）将A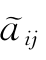＝（）4×5转化成标准矩阵R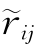＝（）4×5。(www.xing528.com)

（3）假设采用层次分析法对四个属性进行计算后得到相应权重向量为：

w＝（w1，w2，w3，w4）＝（0.25，0.19，0.32，0.24）

（4）通过z＝w R求出各方案的综合评价值分别为：

z1＝[0.36，0.69]；z2＝[0.34，0.54]；z3＝[0.33，0.62]；z4＝[0.34，0.57]；z5＝[0.27，0.49]

可以看出，区间数定量方式层次型风险元传递理论评价后得出的值也不是唯一确定型的值，较传统的综合评价可以给出更多的决策信息，本文接下来给出一种决策排序方案如下。

（5）利用区间数的可能度定义式（2.48）对已经得到的综合评价值进行两两可能度计算，得到可能度矩阵为：

（6）利用式（4.10）对可能度矩阵进行排序可以得到排序向量为：

w＝（w1，w2，w3，w4，w5）＝（0.2330，0.1875，0.2175，0.1965，0.1650）

由此可知方案的排序为：x1＞x3＞x4＞x2＞x5。最优方案为x1。