覆盖粗糙集风险元传递模型的应用

本节提出基于覆盖粗糙集邻域分类器理论的广义项目风险分析的新方法，即以覆盖粗糙集理论为基础、邻域分类器为工具，首先对广义项目风险分析中的历史数据进行归一化预处理，然后应用具有较高分类精度的邻域分类器进行分析，据此建立风险知识库并估计其平均测试精度，最后选择测试精度比较高的风险知识库来预测估计在一组新的风险元测试样本条件下广义项目目标的概率分布，从而探求广义项目目标的风险。最后通过算例分析说明该模型的实用性和有效性。

1.概述

目前广义项目风险分析的方法很多，利用概率统计方法或模糊集方法需要一些数据的先验信息，如概率分布和模糊隶属函数等，有时这些先验信息很难得到。在实际应用时有时掺杂着某些假设条件的人为主观性，因此限制了该类方法在风险分析中的广泛应用。

20世纪80年代由Z.Pawlak提出的粗糙集理论是继概率论、模糊集之后又一种处理不确定性的数学工具，能有效地分析不精确、不一致和不完备的信息，已被成功地应用于机器学习、知识获取、决策分析、知识发现、模式识别、专家系统和决策支持系统等领域。该理论与模糊集理论和概率统计理论最显著的区别是它无需提供问题所需处理的数据集合之外的任何先验信息，因此粗糙集理论较之模糊集理论和概率统计理论在处理不确定性问题上更加具有客观性。

粗糙集理论是建立在分类机制的基础上的，它将分类理解为在特定空间上的等价关系，而等价关系构成了对该空间的划分。由于等价关系或论域上的划分要求过于严格，限制了粗糙集理论在许多实际问题中的应用。因此，人们考虑对粗糙集的等价关系或论域划分进行扩展，其中Zakowski把划分放宽为覆盖，将Pawlak粗糙集理论推广为覆盖广义粗糙集理论。这些年人们对覆盖广义粗糙集理论进行了深入的研究，并得到了不少重要成果。邻域分类器是其中重要的研究成果之一，它本身具有较高的分类精度，具有广阔的应用前景。

基于覆盖粗糙集的风险元传递模型是在前人研究的基础上，以覆盖粗糙集理论为理论基础、邻域分类器为工具，通过从广义项目的风险信息历史数据中进行数据挖掘，进行广义项目风险分析的方法。

2.基于覆盖粗糙集的风险元传递模型

定义3.9　设U是一个非空论域，C是U的一族子集，如果∪C＝U且∀Ci≠Ø，称C是U上的一个覆盖，（U，C）为一个覆盖近似空间。

定义3.10　给定论域U＝{x1，x2，…，xM}，xi∈RN，i＝1，…，M，对于∀xi∈U，B⊆C，xi在子空间中B的邻域δB（xi）定义为：

式中：δ为邻域步长，Δ为度量函数。∀x1，x2，x3∈U，且满足：

（1）Δ（x1，x2）≥0；

（2）Δ（x1，x2）＝0，当且仅当x1＝x2；

（3）Δ（x1，x2）＝Δ（x2，x1）；

（4）Δ（x1，x3）≤Δ（x1，x2）+Δ（x2，x3）。

通常度量函数可以取1-范数，2-范数，∞-范数。显然，C＝∪δB（xi），i＝1，2，…，M为U的一个覆盖，（U，C）为一个覆盖近似空间。

定义（U，A，C，D，F）为广义项目风险信息系统，其中U为广义项目对象集，即：U＝（x1，x2，…，xn），U中的每个元素xi（i≤n）称为一个对象。A为广义项目属性集，即：A＝{a1，a2，…，am}，A中的每个元素aj（j≤m）称为一个属性。为讨论方便，将A划分为A＝C∪D，其中C为广义项目风险元集，即C＝{c1，c2，…，cs}，C中的每个元素cl（l≤s）称为一个风险元；D为广义项目目标集，即D＝{d1，d2，…，dt}，D中的每个元素dk（k≤t）称为一个目标；F为U与A之间的关系集，即F＝{fl：U→Vl（l≤m）}，其中Vl为al（l≤m）的值域。

每个广义项目对象对应的多个风险元值和目标值称为一条记录，表示为Xi（i≤n），即Xi＝[f1（xi），f2（xi），…，fm（xi）]，多条记录构成广义项目历史数据。对于任意的xi（i≤n），定义Z（xi）为对应的目标值。

应用邻域分类器得出风险元传递引起的目标值概率分布的算法步骤如下：

第1步　给定具体化范数m，计算样本对象s所对应的样本向量S与Xi的距离。

第2步　依据邻域的定义，找出S的δ邻域δ（S）。

第3步　若给定阈值Δ，计算落入δ邻域δ（S）满足Z（xi）≥Δ的匹配集F，即：

第4步　计算估计概率P，即：

式中：|F|、|δ（S）|分别表示所对应集合的长度。邻域步长δ计算如下：

式中：w≤1；Xi（i＝1，2，…，n）是训练样本；min[Δ（Xi，S）]表示Xi和测试样本向量S之间的最小距离值；range[Δ（Xi，S）]是Δ（Xi，S）值的范围。在此情况下，邻域步长δ依赖于测试样本对象s周围的局部和全局信息。

3.算例分析

以某电力公司输电线路工程为例，介绍基于覆盖粗糙集理论和邻域分类器的广义项目风险分析的具体过程。

（1）数据描述。引用某电力公司的历史数据，限于篇幅，仅将其中部分数据列出，见表3.15。其中该电力公司输电线路工程的单位投资项对应于项目目标集，而表3.15中的其他所有列对应于项目风险元集，包括地形因素、地形山地、导线型号、地线型号、平均档距、铁塔、水泥杆、人力边距、汽车边距、土石方、挂线金具和绝缘子。(www.xing528.com)

表3.15　某电力公司输电线路工程单位投资及其风险元集历史数据

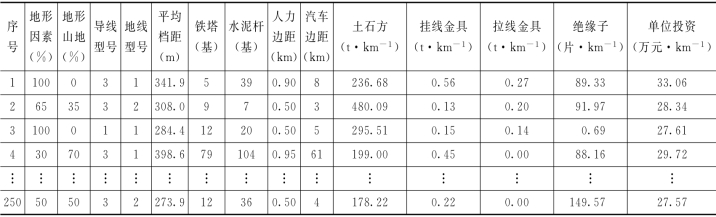
（2）数据预处理。为平衡单个风险元对项目目标的影响程度，需要对历史数据表中的风险元值进行归一化预处理，将其映射到区间[0，1]上，本方法采用最大值映射法。

在本例中历史数据共有250条记录{Xi，1≤i≤250}，很明显，Xi∈R15，i＝1，…，250。由此可得矩阵A250×15＝，将其划分表示为风险元矩阵C250×14和目标向量D250×1。由于仅风险元矩阵影响风险知识库的形成，下面处理主要针对风险元矩阵C250×14。

处理后矩阵Deal250×14中元素Deal[i，j]＝，其中，c[i，j]为风险元矩阵C250×14的第i行第j列元素；max[：，j]为风险元矩阵C250×14第j列的最大值；min[：，j]为风险元矩阵C250×14第j列的最小值，原始数据归一化结果见表3.16。

表3.16　原始数据归一化处理结果

（3）计算测试样本对象s所对应的样本向量S邻域δ（S）。测试样本对象s所对应的样本向量S列表见表3.17。

表3.17　测试样本对象s所对应的样本向量S

依据式（3.90）计算得：邻域步长δ＝1.030（大量实验表明：ω取0.1时，分类效果较好），S的邻域δ（S）见表3.18。

表3.18　测试样本对象s对应的样本向量S的邻域集表

（4）建立风险知识库并估计其测试精度。事实上，由上述风险元矩阵C250×14归一化得到的Deal250×14，加上相对应的目标矩阵D250×1，即构成风险知识库。

考虑到实验数据的随机性，在对风险知识库进行精度估计时，需要进行多次重复分类求平均值即平均测试精度。在此采取循环测试取均值的方法。

依次循环分类取Deal250×14中90%的记录进行测试，为简化运算，本例共取10次，构成测试集，记为Test[i]，i＝1，…，10；相应剩余10%的数据进行匹配，构成训练集，记为Train[i]，i＝1，…，10。

则测试精度η的计算公式为：

其中　

式中：Match（Tj）为训练集Train[i]中训练样本Ti在相应的测试集Test[i]中正确匹配的元素构成的集合。

在Matlab中实现计算，可得各分类精度为：

η＝[0.7788，0.7788，0.7788，0.7788，0.7788，0.8230，0.7345，0.7345，0.7345，0.9074]

平均测试精度即知识的平均精度为：0.7828，如图3.22所示，其中分类编号1～10代表每次分类所产生的风险知识库的测试精度，最后一个直方图灰的表示总体的平均测试精度。为提高广义项目目标值概率估计的准确性，选取上述Deal250×14中单个测试精度最高的测试集Test[10]以及相应的目标向量作为最终的风险知识库。

（5）估计s的风险目标概率。若取阈值Δ，依据式（3.88）计算在所选风险知识库下落入邻域δ（S）满足Z（s）≥Δ的匹配集F，依据式（3.89）求得P（Z（s）≥Δ）的值。随着域值Δ取不同值时，可得测试样本对象s所对应的单位投资Z（s）的概率分布。在Matlab中实现之，结果如图3.23所示，其中横坐标Z（s）表示所取测试样本对象s的单位投资可能取值，纵坐标P代表Z（s）不小于感兴趣的阈值Δ的概率。

图3.22　十次分类的测试精度及平均测试精度直方图

从图3.23中可以看出，曲线的整体趋势，随着阈值Δ的增加，其所对应的P[Z（s）≥Δ]逐渐减小，与实际情况相符合；从曲线上的点看，例如当Δ＝28时，对应的P[Z（s）≥28]＞0.8，而实际对应的单位投资为28.89，可见预测精度比较高，说明了该模型的有效性。

图3.23　测试样本对象s所对应的单位投资Z（s）—P的概率分布

4.结论

本节将基于覆盖粗糙集理论的邻域分类器与广义项目风险元理论相融合，提出了广义项目风险分析的新思路。该模型可以比较有效地预测出广义项目在一组新的风险元测试样本条件下，研究风险元的随机波动对项目目标值的传递影响，探求项目目标值的概率分布。该模型对企业规避风险、合理决策具有重要的参考价值。应该指出，当风险元历史数据量比较大时，该模型的有效性尤为突出。另外，该方法是基于实验测试的，其中邻域步长的取值不同，试验结果也有所变化，究竟在具体的事例中应该取何值效果最佳，还有待于进一步的理论研究和实验测试。目前，该模型主要应用于广义项目的目标集是单目标的情况下，还有待于进一步扩展。