水利防洪工程经济评价风险元传递解析模型及应用探析

水在国民经济中作为一种不可缺少的物质具有利与害的两重性。江河水流所形成的洪水一旦泛滥成灾，损失则很惨重。由于洪水是一种自然灾害，在目前的科学技术与经济水平条件下，要完全控制和免除洪水灾害是不现实的。但在总结多年来治河经验的基础上，积极采取措施，兴建防洪工程，在一定程度上可以减轻或避免洪水损失。

任何防洪工程的兴建，都要进行经济评价，合理的计算与评价方法，应能详尽地考虑防洪效益的特点。防洪效益与水利工程的其他效益相比，具有如下特点：

（1）非增值性。防洪工程不能直接创造财富，而是把兴建工程以后所能减轻或避免的损失视为效益。

（2）随机性。一般的洪水由暴雨造成，暴雨的发生是随机的，相应洪水的形成也是随机的。现在的科学技术还不能预报未来若干年内暴雨和洪水出现的大小和时间。由于水利工程的防洪效益只有在发生大洪水时才能体现出来，没有致灾洪水，也就没有防洪效益。因此，防洪效益也具有随机性。

（3）递增性。社会经济在飞速发展，社会财富也在日益积累，防洪保护区内经济也相应发展。在不同年代发生同频率的洪水，其灾害损失是不相同的，所以防洪工程在经济使用期内其效益随着时间的延长而递增。

1.防洪年效益风险元传递解析计算与分析

由于防洪效益具有随机性，故年效益计算的结果应能够比较准确地描述年效益出现的大小及其可能性，因此，频率法是比较合理的方法。年效益计算的结果是否正确可靠，关键是发生不同频率洪水时灾害的估算方法及其精度，计算出任何频率洪水的淹没范围、淹没深度及淹没历时，进而可以估算出洪水所造成的损失。总之，无论采取何种方法，均需分别求出兴建工程前与兴建工程后灾害损失频率曲线，对应频率的两者相减即可求出工程所减免的灾害损失（即防洪效益）频率曲线。年效益频率曲线比较特殊，它通常具有若干零项，且部分线段非渐变，因此，实用上往往用离散型经验频率曲线表示。

设洪水频率为：p1、p2、…、pm，相应年防洪效益为：b1、b2、…、bm，则年防洪效益的均值为：

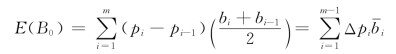
式中：Δpi为两相邻频率之差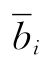；为两相邻频率的防洪效益的平均值。年效益方差D（B0）、均方差σ0及变差系数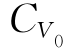分别为：

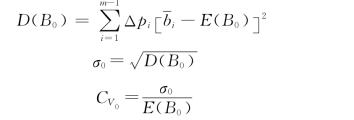
均方差与变差系数均反映了年防洪效益变化的不均匀程度，不均匀程度越大，风险也就越大。在通常情况下，年防洪效益系列的离散程度远大于年洪水系列的离散程度，远远大于年径流系列的离散程度。因此，在防洪经济评价时，进行防洪效益的风险分析是十分必要的。

2.防洪总效益风险元传递解析计算与分析

在防洪工程经济使用期n年内，设年防洪效益系列为：B1、B2、…、Bn，则总效益现值（基准年为开始收益的第一年年初）Z为：

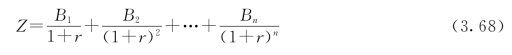
式中：r为经济折现率；Z为随机风险元Bi（i＝1，2，…，n）的函数。

由式（3.68）可知，防洪总效益Z由计算期内各年效益解析计算而得，则防洪总效益的变化特征是由年效益的变化特征、计算期n及折算率r所共同决定的。年效益的随机变化规律难以用理论频率曲线来拟合，它通常可以概化为离散型的经验频率曲线，若离散的状态数目为m个，则在计算期n年内，n个m值的组合状态数为mn个，如此浩大的状态组合数目（如m＝7，n＝40，则740≈6.37×1033），要分别计算它们的总效益及出现的频率，即使利用计算机也难以实现。因此，直接计算总效益Z的频率曲线是不可取的。

笔者在分析防洪效益特点的基础上，提出如下风险元传递的解析算法。

若年效益频率曲线的离散状态数为m，则总效益有mn种可能结果，在所有结果中，总效益Z的下限值为零。显然这mn种结果必然构成一种概率密度曲线，笔者认为，可用P-Ⅲ曲线拟合。P-Ⅲ型分布的概率密度函数为：

如果假定Cs＝2CV，则关键问题是确定Z的期望值E（Z）及方差D（Z）。

由于年际之间洪水的发生是相互独立的，故年防洪效益之间亦相互独立。依据多元随机变数的有关性质，对式（3.68）两边分别取数学期望与方差，得：

防洪效益具有递增性，设多年平均递增率为f，基准年年效益B0为风险元，则有：

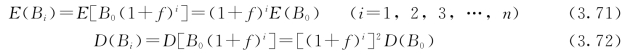
将式（3.71）和式（3.72）分别代入式（3.69）和式（3.70），得出风险元传递解析公式为：(www.xing528.com)

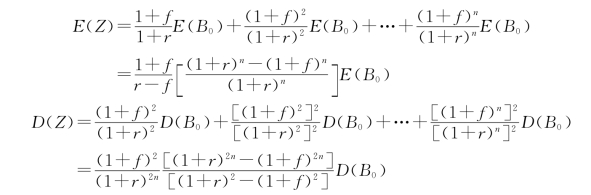
式中：为风险传递系数。

Z的均方差及变差系数分别为：

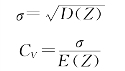
至此，P-Ⅲ分布的三个基本参数E（Z）、CV和Cs均已确定，据此可以求出防洪总效益Z与累积概率P的关系。这条关系曲线，完整地描述了总效益的变化规律，它所提供的信息，比现行的仅计算期望值所提供的信息多得多。

比较完善的决策方法应当是，依据上述Z—P关系及防洪工程所分摊的投资、运行等所有费用现值来计算经济评价指标（如净现值、效益费用比等）的频率曲线，有了这条频率曲线，也就有了期望值的大小以及还本累积概率的大小，评价工程的经济可行性应从这两方面来综合考虑。若对防洪工程的不同方案进行比较，其一可以比较期望值的大小，其二可以比较还本的累积概率，还本的累积概率不应小于某一下限值，其下限值的大小（例如80%）应在规范中统一规定；小于该下限制的方案为不可行方案，在可行方案中再比较期望值的大小，取其大者作为最优方案。

3.应用实例

拟建某综合利用水库，水库建成后担负下游防洪任务。通过历史洪水灾害的调查以及不同频率洪水发生时的水文水利计算，分别确定工程前后相应不同洪水频率的损失，进而求出基准年相应于不同频率的防洪效益。

（1）防洪年效益风险元传递解析计算与分析。洪水频率Pi：0～0.01、0.01、0.02、0.05、0.10、0.20、0.25、1.0。相应防洪效益bi（万元）：400、7000、4000、2000、1000、600、0、0。则相邻频率段内效益的均值为：

Δpi：0.01，0.01，0.03，0.05，0.10，0.05，0.75

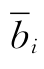：400，5500，3000，1500，800，300，0

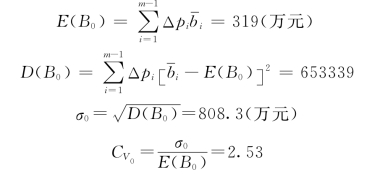
由此可知，年防洪效益的离散程度是相当大的。

（2）防洪总效益风险元传递解析计算与分析。取多年平均递增率f＝0.02，经济折现率r＝0.06，工程经济使用期n＝40年，则有：

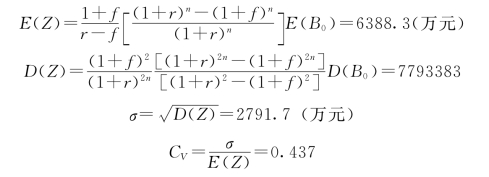
Cs＝2CV＝0.874

由已知的E（Z）、CV、Cs即可求出总效益Z—累积频率P的关系。令φ＝，则Z＝E（Z）+φσ，由已知的Cs及拟定的一组P分别查P-Ⅲ型分布φ值表[141]，求得Z—P的关系数据如表3.12所示。基于表3.12数据，借助统计软件SPSS 13.0，绘制Z—P的关系曲线如图3.20所示。

表3.12　总效益Z—累积频率P的关系

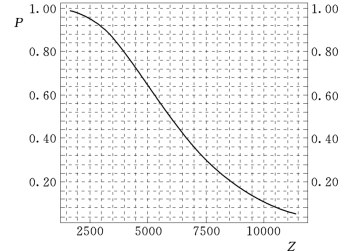
图3.20　总效益Z—累积频率P的关系曲线

从P—Z的关系可知，工程防洪总效益大于等于期望值（6388.3万元）的机会只有45%，显然，仅仅依据期望值作决策，是不太合理的。

若还本累积频率的下限值为0.80，则工程总费用的现值小于4015万元为可行方案，否则为不可行方案。假设本工程总费用现值为6000万元，按照传统的计算与分析方法，其净效益为388.3万元，效益—费用比为1.06，为可行方案。但该方案实施时还本的累积概率只有50%，即出现风险的概率为50%，不符合规定的还本累积概率，为不可行方案。

水利防洪工程的风险表现为两个方面，一是在工程使用年限内特大洪水发生次数较少，工程的防洪效益没有体现出来，防洪工程没有达到预期效果；二是在工程使用年限内，发生超标准的特大洪水，致使工程失事。对于大中型水库，虽然其失事的可能性极小，但在工程可行性研究阶段也应当考虑。目前防洪工程的经济评价均未考虑上述两方面的风险，而上述模型仅对第一方面的风险进行了分析。

上述防洪工程风险分析方法，考虑了洪水的随机变化对防洪工程经济效果的影响，采用概率分布方式更加客观地描述防洪效益的随机变化规律，提出采用期望值及还本的累积概率两方面为依据作决策，其决策效果比传统的期望值决策法更加科学合理。