水力发电工程经济评价风险传递解析模型及应用

任何拟建的水力发电工程，在投资前必须进行经济评价。经济评价的主要内容是预估方案的费用和效益，并计算表示其经济效果的各项指标，以论证工程在经济上的可行性。水力发电工程经济效益主要取决于发电量，而发电量受来水等随机性因素的影响，具有随机变化的特征，因而水力发电效益也具有随机变化的特征，合理的经济计算与评价方法应对这种随机变化的特征进行周详的考虑。在分析和评价水力发电工程的经济效益时，传统方法认为各年的效益是相等的，并采用唯一确定的数据。即用一个均匀的效益系列来代替实际发生时不均匀的随机效益系列，这种代替所产生的误差是不容忽视的。

本节基于理论价格法计算水力发电效益，提出将年发电量作为风险元的风险型年效益计算模型，给出通过丰、平、枯三个典型年的年发电量来估计年发电量变化的期望值、方差和变差系数的解析模型。在年效益计算的基础上，依据多元随机变数的有关理论，通过建立风险元传递解析模型，推求水力发电工程经济计算期内总效益的概率分布特征参数，进而推求总效益的概率分布。该方法考虑了来水的随机变化对水力发电工程经济效果的影响，采用概率分布方式更加客观地描述水力发电效益的随机变化规律，为水力发电工程项目的合理决策提供更加科学、合理的依据。

1.水力发电工程年效益风险元传递解析计算与分析

用理论价格法计算水力发电效益，其年效益主要取决于年发电量，而年发电量受许多因素制约。在水库规模和水电站装机容量均已确定的情况下，年发电量主要取决于年内用于发电的流量过程及其相应的水头过程。流量及水头在不同年份具有不同的变化过程，这是因为不同年份的年径流量是一种服从偶然性规律的随机变量。而对于大多数水头较高的水电站，均遵循水力发电量最大的最优运行准则，遇多水年份，用于发电的水量也多，水头也比较大，相应年发电量也大；反之则相反。这说明在通常情况下，年发电量与年来水量具有同步的随机变化特性，因而年发电效益与来水量也具有同步的随机变化特性。

在水库正常蓄水位、死水位、年来水量及水电站装机容量均已确定的情况下，用理论价格法计算水力发电年效益的公式为：

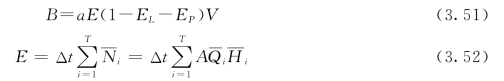
式中：B为年发电效益；a为有效系数；E为年发电量，k W·h；EL为线损率；EP为发电厂用电率；V为度电的理论价格（或影子价格）；Δt为计算时段内小时数，h；T为年计算时段数（＝8760/Δt）；Ni为年内第i时段平均出力（i＝1，2，…，T），k W；A为出力系数，A＝9.81η，η为机组总效率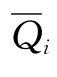；为第i时段平均流量（i＝1，2，…，T），m3/s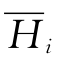；为第i时段平均净水头（i＝1，2，…，T），m。

由已知的来水过程及其他资料即可求得年发电量。那么，在经济计算期n年内，由n年的来水过程即可求得n年内各年的发电量。实际上，在规划和可行性研究阶段，由于来水过程的随机性，不可能得知未来若干年内天然来水的过程。在这种情况下，通常采用时历法或统计模拟法来预估。由这两种方法描述的未来径流过程，与未来真实的过程显然不会相符，但由这两种方法提供的径流系列所服从的统计规律完全可以代表未来真实系列的统计规律。例如，由过去实测径流系列所推求的统计特征参数——期望值和方差，可以代表未来若干年内径流变化过程的期望值和方差。依据这种原理，可由时历法或统计模拟法提供的长系列水文资料来推求年发电量变化的特征值。其方法有如下两种。

（1）长系列操作法。这种方法是用m个年的水文系列资料，逐年逐时段调节计算，求得m个年发电量值E1、E2、…、Em，由这m个年发电量值即可求得年发电量变化的均值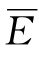、方差D（E）及均方差σE。

（2）丰、平、枯三点（年）法。所取三点（年）的频率P1、P2、P3可根据来水资料占据频率的范围，选用（3%、50%、97%）、（5%、50%、95%）、（10%、50%、90%）等。由于年发电量同年径流量具有同步的随机变化特性，可以认为年发电量的变化同年径流量一样也服从皮尔逊Ⅲ型（简称P-Ⅲ型）分布。问题是，如何依据三个典型年的年发电量值来推求年发电量E变化的期望值、方差（或均方差）及偏差系数Cs是关键。

已知P-Ⅲ型分布的离均系数是P及Cs的函数，由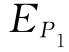、、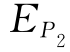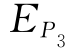可建立如下联立方程：

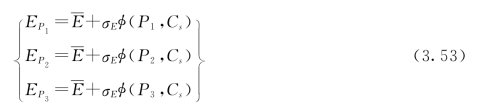
令

并定名S为偏度系数。将式（3.53）代入式（3.54）后可知S是Cs的函数，可根据式（3.54）计算出的S值从三点法用表——S与Cs关系[141]表中查得Cs值。再由式（3.53）解得：

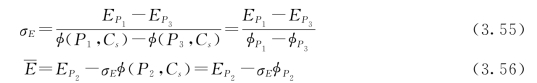
式中：及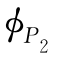只与Cs有关，可通过查表[141]（三点法用表——Cs与φP值关系）得到。在用上述两种方法求得年发电量变化的均值和方差（或均方差）后，对式（3.51）分别取数学期望及方差，可求得年发电效益的期望值E（B）、方差D（B）及均方差σB分别为：

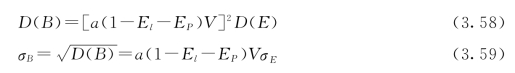
年效益的期望值反映了年效益变化的平均情况，而方差或均方差反映了年效益变化的不均匀程度。不均匀程度越大，风险越大。

2.水力发电工程总效益风险元传递解析计算与分析

在水力发电工程经济计算期n年内，设年发电效益系列为：B1、B2、…、Bn，则总效益现值（以开始受益的年份为基准年）Z可用式（3.60）计算：

式中：r为社会折现率。

由Bi的概率分布推求Z的概率分布，可以采用蒙特卡洛模拟法。考虑到对计算方法力求简单、便于提供数据和便于推广应用的要求，采用风险元传递解析计算法。

前已述及，不同年份的年径流量是相互独立的随机变量，因而，不同年份的年发电效益也是相互独立的（即相关系数ρ＝0）。依据多元随机变数的有关理论，对式（3.60）分别取数学期望及方差，得：

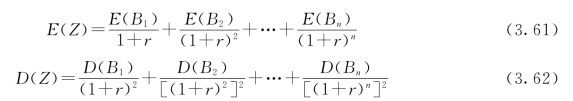
由于年径流量的变化过程是具有平稳性的随机变化过程，所以年发电效益的变化过程也具有平稳性，即各年服从同一分布：

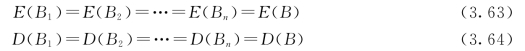
将式（3.63）和式（3.64）分别代入式（3.61）和式（3.62），整理后得：(www.xing528.com)

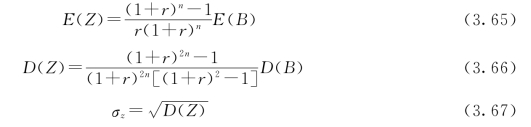
式中：为风险传递系数；σz为Z的均方差。式（3.66）即为风险传递公式。

为了推求水力发电工程总效益Z的概率分布曲线，需要用某一理论分布函数来描述总效益的变化规律。笔者认为，总效益Z近似服从正态分布。这一结论从如下的分析得出。前已述及，年发电效益所服从的分布同年径流量一样，为P-Ⅲ型分布，但其不对称程度要减小，即年发电效益概率分布的Cs值一般比年径流量概率分布的Cs值要小。这是因为遇特丰年份，年发电量受装机容量限制，不能发出特别多的电能；遇特枯年份，水电站为保证电量供应，会尽最大可能发电。调节性能越强的水库，上述现象越显著。由概率论中特征函数的性质可以证明，独立的n个服从P-Ⅲ型分布具有相同参数α和β的变量之和（即水力发电工程总效益）也服从P-Ⅲ型分布，其参数为βn＝β、αn＝nα，已知α与Cs的关系为α＝4/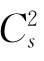，则αn＝nα＝4n/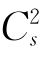，Csn＝2/。由此式可知，总效益概率分布的偏态系数Csn比年效益的Cs值要小得多，说明其分布接近于正态。因此，笔者认为，用正态分布来描述水力发电总效益Z的变化特征是合适的。

上面已经求出了总效益变化的期望值E（Z）、方差D（Z）及均方差σZ，由E（Z）及σZ这两个特征参数即可描绘出水力发电总效益Z的概率分布曲线。

3.经济效果风险元传递解析计算与分析

工程经济效果决定于工程的总效益及总费用。如上所述，工程的总效益受不确定因素的影响，具有随机性，可用概率分布曲线来描述；而工程的总费用，虽然也是不确定的，但这种变化主要受人为因素的影响，随机特性不明显。因此，在经济效果的风险分析时，将费用视为常数，设费用现值为IP，则依据总效益概率分布曲线及IP可求得效益费用比R0（R0＝Z/IP）、净现值NPV（NPV＝Z-IP）等经济评价指标的概率分布曲线。有了这些分布曲线，也就有了风险发生的各种信息。例如：从这些曲线可以得知经济效果变化的期望值是多少，亏本的风险率是多少等信息。这比仅计算唯一确定值所提供的信息要全面得多，决策者依据这些信息做决策，会更加合理得当。

本方法仅将年发电量作为随机风险元，推出了工程经济评价指标的概率分布曲线。至于度电价格、工程费用等其他不具有随机特性或随机性不明显的不确定因素对工程经济评价指标的影响，宜作敏感性分析。其方法为：在进行风险（概率）分析时，分别采用这些因素的不同浮动值，求得不同的经济评价指标的概率分布曲线，进而求得不同的盈利概率或亏本的风险率等信息。这样能比较全面地揭示各种不确定因素对水力发电工程经济效益的影响，为水力发电工程的合理决策提供可靠依据。

4.应用实例

拟建某大型水库，水库以发电为主。水库具有年调节能力，水力发电工程的总费用现值为15.5亿元。水电站装机容量为40万k W，发出的电直接送至大电网，线损率El取7%，厂用电率EP取2%，有效系数a取1.0，度电理论价格V取0.20元，社会折现率r取10%，经济计算期n以40年计。

（1）年效益风险元传递解析计算与分析。

1）年发电量概率分布特征参数的推求。已知水库坝址处具有30年的实测水文资料，拟采用丰、平、枯三点法来推求年发电量概率分布的特征参数。通过对30年水文资料的统计分析得出：频率P为5%的丰水年、P为50%的平水年、P为95%的枯水年三个典型年的年径流量分别为2306亿m3、1045亿m3、384亿m3。对这三个典型年采用图解法分别进行逐时段调节计算，求得三年的年发电量分别为：E5%＝17.2亿k Wh，E50%＝9.83亿k Wh，E95%＝4.53亿k Wh。

根据式（3.54）得：＝0.163。查三点法用表——S与Cs关系表，得：Cs＝0.60。查三点法用表——Cs与φP值关系表，得：φ5%-φ95%＝3.259，φ50%＝-0.100。由式（3.55）及式（3.56）可得：

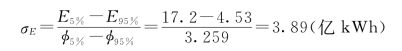
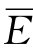＝E50%-σEφ50%＝9.83-3.89×（-0.100）＝10.22（亿k Wh）

2）年发电效益概率分布特征参数的推求。由式（3.57）及式（3.59）得：

E（B）＝a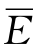（1-El-EP）V＝1.0×10.22×（1-0.07-0.02）×0.20＝1.860（亿元）

σB＝a（1-El-EP）VσE＝1.0×（1-0.07-0.02）×0.20×3.89＝0.708（亿元）

D（B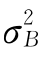）＝＝0.5012

（2）总效益风险元传递解析计算与分析。由式（3.65）及式（3.66）得：

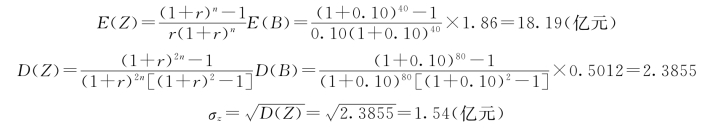
由E（Z）及σz即可描绘总效益Z的概率分布曲线。

（3）经济效果评价指标的风险分析。净现值NPV的期望值、均方差分别为：

E（NPV）＝E（Z）-IP＝18.19-15.5＝2.69（亿元）

σNPV＝σZ＝1.54（亿元）

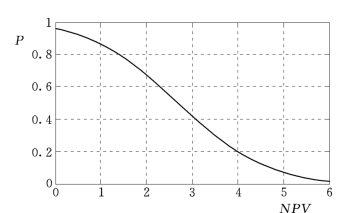
图3.19　净现值NPV与大于NPV的概率P的关系曲线

由E（NPV）及σNPV即可求出净现值NPV与大于NPV的概率P的关系曲线。借助数学计算软件Matlab，绘制NPV—P的关系曲线如图3.19所示。

从图3.19可知，工程盈利（即工程净现值大于零）的概率为96.0%，则工程亏本的概率（即风险率）为4.0%，净现值期望值为2.69亿元，大于该期望值的概率为50%。该工程净现值期望值及盈利的概率均比较大，方案是可行的。

（4）结论。依据多元随机变数解析法原理，在水力发电工程项目年效益风险分析、总效益风险分析的基础上，通过风险元传递计算，推出了净现值NPV的概率分布的特征参数，基于该特征参数，可以绘制净现值变化的概率分布曲线。依据该曲线可以掌握净现值变化的大致范围、分布中心、盈利的概率、亏本的风险率等信息，这与传统的计算方法所求得的唯一确定值相比，考虑了风险因素，更符合客观实际。