NPV与基准折现率的风险互动关系

NPV和基准折现率i之间的函数关系为：

当t为高次项时，基准折现率i很难写成由NPV表示的显函数形式，因此当考虑风险因素后，将基准折现率i作为随机风险元，很难用传统概率论与数理统计理论进行传递计算，进而得出NPV的相关分布或参数与基准折现率之间的关系，这时需要借助判断函数的单调性来实现其相关传递的推导。

定理3.3　若因变量和自变量之间在某一定义域内存在严格单调递增关系，即对于自变量x的某一定义域内任意两点取值，若存在x1＜x2，恒有y1＜y2，则在此定义域内有以下结论成立：FY（y）＝P{Y≤y}＝P{X≤x}＝FX（x）。

证明：分别记因变量Y和自变量X的分布函数为FY（y）和FX（x），根据概率论，有：

FY（y）＝P{Y≤y}＝P{f（X）≤y}

由于目标对象Y和自变量X满足严格单调关系，因此传递函数存在反函数，并且反函数仍然单调。因此有：

P{f（X）≤y}＝P{X≤f-1（y）}＝P{X≤x}＝FX（x）

因此，定理3.3得证。

定理3.4　若因变量和自变量之间在某一定义域内存在严格单调递减关系，即对于自变量x的某一定义域内任意两点取值，若存在x1＜x2，恒有y1＞y2，则在此定义域内有以下结论成立：FY（y）＝P{Y≤y}＝P{X≥x}＝1-P{X≤x}＝1-FX（x）。

证明：分别记目标对象Y和自变量X的分布函数为FY（y）和FX（x），根据概率论，有：

FY（y）＝P{Y≤y}＝P{f（X）≤y}

由于目标对象Y和自变量X满足严格单调递减关系，因此传递函数存在反函数，并且反函数仍然单调递减。因此有：

P{f（X）≤y}＝P{X≤f-1（y）}＝P{X≥x}＝1-P{X≤x}＝1-FX（x）

因此，定理3.4得证。

基于上述定理，若给出NPV和基准折现率i之间的单调性关系，则可以得到相应的传递关系，因此给出以下定理。

定理3.5　当min[（CI-CO）t]≥0（t＝0，…，n）时，NPV和基准折现率i之间满足严格单调递减关系。

定理3.6　当max[（CI-CO）t]≤0，（t＝0，…，n）时，NPV和基准折现率i之间满足严格单调递增关系。

证明：净现值和内部收益率的关系如下：

∀i1＞i2≥0，有：

∵t＞0，i＞0

∴（1+i）-t是单调减函数(www.xing528.com)

∴（1+i1）-t＜（1+i2）-t

∴（1+i1）-t-（1+i2）-t＜0

1）若min[（CI-CO）t]≥0，t＝0，…，n，且Ǝ（CI-CO）t≠0，t＝0，…，n

则：

因此：NPV1＜NPV2

故定理3.5成立。

2）若max[（CI-CO）t]≤0，t＝0，…，n，且Ǝ（CI-CO）t≠0，t＝0，…，n

则：

因此：NPV1＞NPV2

故定理3.6成立。

对于净现金流符号只变化一次的常规投资项目，即在项目寿命期初（投资建设期和投产初期）净现金流量一般为负值，项目进入正常生产期后，净现金流量变为正值的项目，设当t＝k，t∈[1，n]，k＜n时净现金流量发生变化，则式3.50可作如下变换：

更一般的，对于投资时间多于两期（n＞2）的常规投资项目，假设在第k（2≤k＜n）年净现金流量发生符号上的改变，则有以下推论成立。

推论3.1　对于一次投资的常规投资项目，即项目寿命初期第一年一次投资项目，NPV和基准折现率i之间满足严格单调递减关系。

证明：由题设可知，项目净现金流可以写成下式：

当t＝0时，由NPV和IRR的关系可知，第一年的一次投资为NPV函数的常数项，并不影响NPV和基准折现率i之间的单调关系，由定理3.5可知，推论3.1成立。

推论3.2　当0≤i≤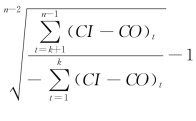时，NPV和基准折现率i之间满足严格单调递减关系。

证明：

因为NPV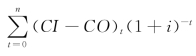＝，求导，有：

若NPV和基准折现率i之间满足单调递减关系，则需≤0。即：

因此，推论3.2得证。