探究经济评价指标中内部收益率风险元传递的解析模型

选择内部收益率IRR作为经济评价指标，IRR是项目净现值为零时的折现率，其表达式为：

式中：CI为现金流入；CO为现金流出。令（CI-CO）t＝Ft，Ft为净现金流量；为了计算简便，令（1+IRR）-1＝y，则IRR＝y-1-1，这样式（3.31）可改写为：

用内插法可求出y＝y0，则可求出IRR0；或通过查表可直接求出IRR0。

本方法讨论多个因素同时变动对经济评价指标IRR的影响。假设变化因素有m个，即项目中存在m个风险元，且各个风险元的变化量为x1，x2，…，xm。当这m个风险元同时变化，必然引起净现金流量Ft的变化，即：

令P（x1，x2，…，xm，y）＝Ft（x1，x2，…，xm）yt＝0，这里y是x1，x2，…，xm的隐函数，即y＝y（x1，x2，…，xm），函数y（x1，x2，…，xm）可视为各个风险元对经济评价指标的传递函数。

如果各个风险元的变化量x1，x2，…，xm不大时可选择全微分法计算y的变化dy，从而求出风险元的传递函数。当各个风险元的变化量由（0，0，…，0）变化为（x1，x2，…，xm）时，由全微分定义求得dy在（0，0，…，0）的全微分：

由于各个风险元变化量x1，x2，…，xm不大时，x1，x2，…，xm可近似等于dx1，dx2，…，dxm，则式（3.34）可改写成：

式中：可视为各个风险元对经济评价指标的传递系数。由隐函数可微性定理得：

则式（3.34）可改写为：

当取（x1，x2，…，xm）为（0，0，…，0）时，y＝y0。将（0，0，…，0）、y0代入式（3.38）中，得到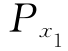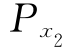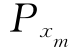，，…，，Py，再将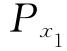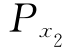，，…，Pxm，Py和（x1，x2，…，xm）代入式（3.37）中，即可求得dy的解析表达式：

其中　

接下来，可以通过各个风险元变化的概率分布及其特征参数得出项目经济评价指标的概率分布及其特征参数，从而得出风险元是如何传递和影响项目的风险的，这里假设各个风险元的变化量是相互独立的。(www.xing528.com)

根据概率论中随机变量函数的数字特征的有关定理，对式（3.39）等号两边同时取数学期望，得dy的数学期望E（dy）的公式为：

其中　E（dy）＝μ

对式（3.39）等号两边同时取方差，得dy的方差D（dy）的公式为：

由式（3.40）、式（3.41）可以看出项目风险定量表征的大小是由风险的传递系数和各个风险元概率分布的特征参数决定。这样，如果有了项目风险变化的数学期望E（dy）及方差D（dy）这两个特征参数，也就有了风险分析的关键信息，因为在大多数情况下这两个特征参数可以决定其项目风险变化的概率分布。根据实际经验可知，在大多数情况下，dy服从正态分布，因为项目的风险通常受许多因素的影响，而每个因素影响的大小往往难以确定，但是通常越靠近期望值数据越集中，因此认为项目目标服从正态分布是最合适的。于是可以得出dy的概率密度函数，即：

其中　E（dy）＝μ，D（dy）＝δ

由dy＝（1+ΔIRR）-1可求出ΔIRR的概率分布函数。

若ΔIRR＜-1，则ΔIRR的概率分布函数为：

若ΔIRR＞-1，则ΔIRR的概率分布函数为：

若ΔIRR＝-1，dy无意义，这里不予考虑。

然后可以用Matlab作出ΔIRR的分布情况的图形。