工程盈利可靠性及投资回收期的应用实例

拟建某大型水库，水库以发电为主，对水力发电工程的总效益、总费用及各项经济评价指标作风险元传递解析计算。预计该工程建设项目将于2009年4月动工，2013年年底竣工，2014年开始受益，社会折现率r以10%计，经济计算器n以40年计。

将水库工程的年效益作为随机风险元，通过对年效益的概率估计和分析，求得如下数据：年发电量变化的期望值为10.22亿k Wh，均方差为3.89亿k Wh；年发电效益变化的期望值E（B）为1.860亿元，均方差σB为0.708亿元，各年服从同一概率分布。

根据建设施工计划，在正常情况下各年需工程投资K见表3.4。

表3.4　工程投资计划表

1.总效益现值的风险元传递解析计算

在已知年效益期望值和方差的情况下，由式（3.12）和式（3.13）可求得总效益现值B0的期望值E（B0）和方差D（B0），分别为：

则均方差：

2.总费用现值的风险元传递解析计算

（1）总投资现值的风险元传递解析计算。采用概算编制办法所得出的客观估计值与专家组的主观估计值相结合，给出各项子投资费用最小、最可能、最大三个特征值，据此，概化为三角形分布，求得统计特征参数的期望值和均方差，见表3.5。

表3.5　各项子投资费用期望值和均方差一览表

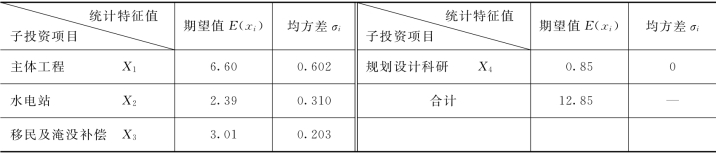
通过分析，认为各项子投资间没有共同的影响因素存在，故取各项子投资间的相关系数为零，这样，依据式（3.19）和式（3.20）可以求得总投资现值K0的期望值E（K0）和方差D（K0）分别为：

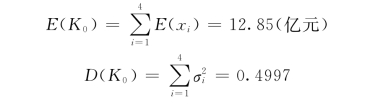
则均方差为：

变差系数为：

C＝σ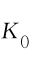/E（K0）＝0.055

（2）总运行费现值的计算。预估各年的年运行费Ci均为0.30亿元，则总运行费现值C0为：

计算得总费用现值为：

K0+C0＝12.85+2.93＝15.78（亿元）

3.净现值的风险元传递解析计算

由式（3.22）及式（3.23）即可求得净现值NPV变化的期望值E（NPV）及方差D（NPV）分别为：

E（NPV）＝E（B0）-E（K0）-C0＝18.19-12.85-2.93＝2.41（亿元）

D（NPV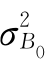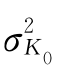）＝+＝2.3855+0.4997＝2.8852

则NPV的均方差为：

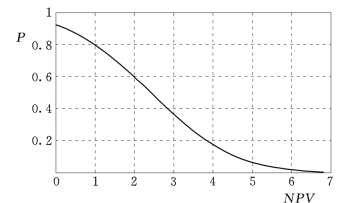
图3.7　净现值NPV与大于NPV的概率P的关系曲线

由E（NPV）及σNPV这两个特征参数即可绘制净现值NPV—P（大于NPV的概率）的关系曲线。借助数学计算软件Matlab，绘制NPV—P的关系曲线如图3.7所示（具体绘制方法详见第7章）。

从NPV—P的关系可知，净现值NPV大于零的概率P即工程盈利的概率为92.3%，则工程亏本的风险率为7.7%。净现值期望值为2.41亿元，大于该期望值的概率为50%。该工程净现值期望值及盈利的概率均比较大，方案是可行的。

4.效益费用比的风险元传递解析计算

由式（3.27）及式（3.28）可以求得效益费用比R0的期望值E（R0）及方差D（R0）分别为：

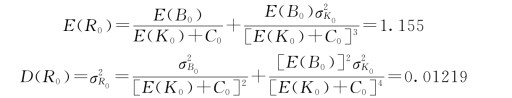
则均方差为：

由E（R0）及σR0两个特征参数，借助Matlab软件，即可求得效益费用比R0—P（大于R0的概率）的关系点据，见表3.6。

表3.6　效益费用比R0—大于R0的概率P的关系表

从R0—P的关系表可知，效益费用比R0大于1.0的概率P，即工程盈利的概率P为92.1%，那么工程亏本的概率P为7.9%。这一结论与净现值的结论相近。

5.内部收益率的风险元传递解析计算

拟定如下一组内部收益率（IRR）值：0.09，0.10，0.11，0.12，0.13。如拟定IRR＝0.09，即取r＝0.09。

（1）总效益现值B0。

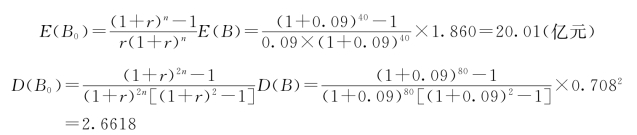
则均方差为：

(www.xing528.com)

（2）总投资现值（K0）。

E（K0）＝2.01×1.095+2.6×1.094+2.6×1.093+1.2×1.092+0.81×1.09

＝12.44（亿元）

可以理解，总投资现值（K0）的变差系数（CV）不随IRR变化，则均方差为：

σ＝CE（K0）＝0.055×12.44＝0.684（亿元）

（3）总运行费现值（C0）。

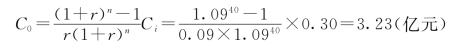
由式（3.22）及式（3.23），可以求得E（NPV）及D（NPV），分别为：

E（NPV）＝E（B0）-E（K0）-C0＝20.01-12.44-3.23＝4.34（亿元）

D（NPV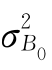）＝+＝1.632+0.6842＝3.125

则：

由E（NPV）及σNPV即可求得净现值（NPV）大于零的概率P，通过Matlab软件，求得P为99.4%，即内部收益率（IRR）大于0.09的概率为99.3%。

用同样的方法可以求得内部收益率（IRR）大于其他拟定值的概率P，其计算结果汇总于表3.7。

表3.7　内部收益率概率分布曲线计算结果汇总表

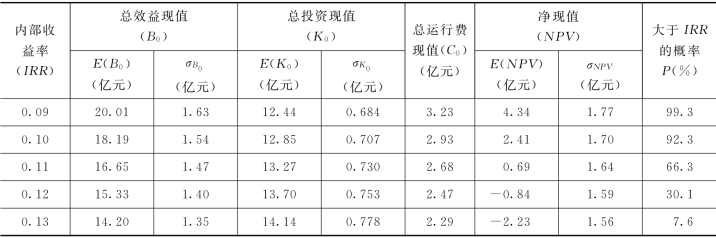
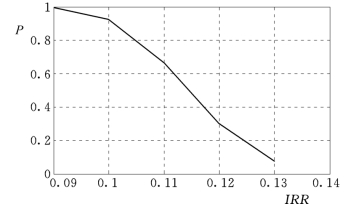
图3.8　内部收益率IRR—P（大于IRR的概率）的关系曲线

点绘表3.7中的IRR—P的关系曲线，即内部收益率IRR的概率分布曲线，如图3.8所示。若规定的最小内部收益率IRR′为10%，则从表3.7可知，工程盈利（IRR＞IRR′）的概率为92.3%，则工程亏本的风险率为7.7%。在通常情况下，内部收益率IRR在0.10～0.13之间变动，小于0.10的概率为7.7%，大于0.13的概率为7.6%，在0.10～0.13之间变动的概率为84.7%。

6.投资回收期的风险元传递解析计算

（1）求投资回收期的近似期望值E（TD）。根据式（3.30）得：

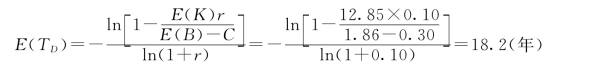
说明投资回收期在18.2年两侧波动。

（2）在期望值两侧拟定一组投资回收期值，并计算小于拟定值的概率。如拟定投资回收期值：8，10，12，14，16，18，20，22，25，30，35，40，50。将这些拟定的投资回收期分别作为计算期，推求净现值变化的期望值E（NPV）及方差D（NPV），进而推求净现值大于零的概率P，该P即为投资回收期小于拟定回收期的概率，从而求得TD—P关系。

1）如拟定TD＝18年，即计算时取n＝18年，由式（3.12）、式（3.13）即可求得总效益现值的期望值E（B0）、方差D（B0）分别为：

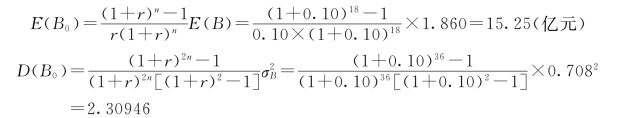
则均方差为：

2）总投资现值的期望值E（K0）及均方差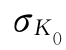不随n的大小而变化，即E（K0）＝12.85亿元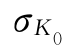，＝0.707亿元。

3）18年内折算总运行费现值C0为：

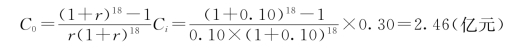
由式（3.22）、式（3.24）即可求得净现值变化的期望值E（NPV）和方差D（NPV）分别为：

E（NPV）＝E（B0）-E（K0）-C0＝15.25-12.85-2.46＝-0.06（亿元）

D（NPV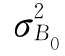）＝+＝1.522+0.7072＝2.8102

则均方差为：

由E（NPV）及σNPV这两个特征参数即可求得净现值大于零的概率。通过Matlab软件求得净现值大于零的概率P为48.6%，该值也就是投资回收期小于18年的概率。

用同样的方法，可求得当投资回收期分别为8年、10年、12年、14年等时的净现值大于零的概率。计算结果汇总于表3.8。

表3.8　投资回收期概率分布曲线及概率密度曲线计算结果汇总表

注 a为接近于0的概率值。

（3）采用Matlab软件点绘（具体绘制方法详见第7章）表3.8中的TD—P关系曲线，该曲线即为TD的概率分布曲线，如图3.9所示。从表3.8中小于TD的累积概率点据可以求得相邻回收期间的概率密度，进而求得单位年份的概率密度，由此可以点绘TD的概率密度曲线，如图3.10所示。

图3.9　投资回收期TD—P（小于TD的累积概率）的关系曲线

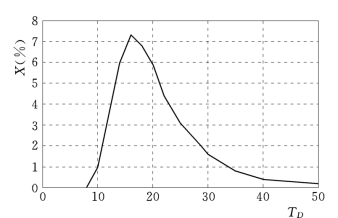
图3.10　投资回收期概率密度曲线

从表3.8和图3.9可知，该工程在经济计算期40年内，工程的投资可以回收的概率为92.3%，那么，不能回收即亏本的概率为7.7%；在25年内可以回收投资的概率为78.3%；在18年内可以回收投资的概率为48.6%。从图3.10可知，投资回收期的概率密度曲线为非对称的正偏分布，其众值在第15年左右，说明在第15年左右回收投资的可能性最大，在14～16年间投资可以回收的概率为14.6%，在12～20年间投资可以回收的概率为51.8%。总之，只要掌握了TD的概率分布及概率密度曲线，也就掌握了在任何年内投资可以回收的概率等信息。这与传统的确定性方法计算的唯一回收期相比，提供了更多的信息，为合理决策提供了更多可靠的科学依据。