应用实例：企业投资收益率风险分析与评估

设新建一个企业，其基本指标如下：投资费用为T万元，设计能力年产量为W台，生产能力利用率为L，单位产品销售价格为B万元，单位产品原材料成本为C万元，年工资费用为K万元，年折旧费为D万元，年管理费为S万元，销售产品税率为t。产品不存在销路问题，则在上述条件下，该企业的投资收益率R的表达式为：

1.风险元的概率估计

把年产量W、单位产品销售价格B、单位产品原材料成本C以及生产能力利用率L作为风险元，其他参数均作为确定值处理。已知T＝500万元；K＝66.25万元；D＝51.75万元；S＝57.0万元；t＝5%。通过主观的和客观的估计，给出各风险元的概率分布及其特征参数见表3.2。

表3.2　各风险元的概率分布及其特征参数

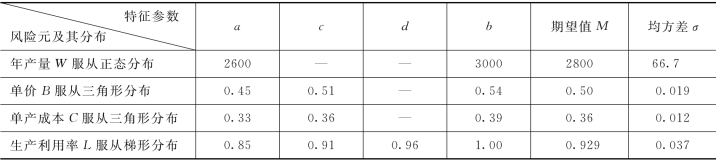
2.风险元的相关分析

通过相关分析，给出风险元之间的相关系数矩阵为：

3.投资收益率R的风险传递计算

期望值E（R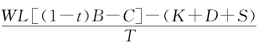）＝＝24.8%。

方差的表达式及其计算结果如下：

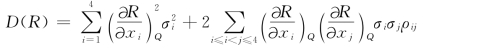
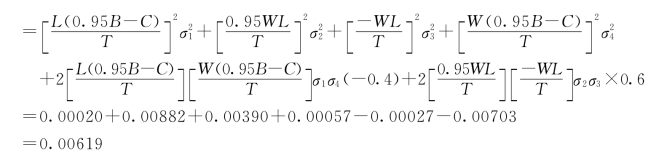(www.xing528.com)

则均方差：

从组成D（R）的式子分析可知：传递风险的关键性风险元是单位产品价格B和单位产品成本C，这两个风险元所产生的风险占总风险的92%。因此，提高产品售价和降低产品成本是企业盈利的关键所在。

4.投资收益率R—累积概率P关系曲线的绘制

在假设投资收益率R服从正态分布的前提下，由期望值E（R）和均方差σR，借助数学计算软件Matlab，即可计算表3.3所列的部分点据，并利用该软件绘制R—P关系曲线，如图3.6所示（利用Matlab绘制概率分布图详见第7章）。

表3.3　投资收益率R—累积概率P关系表

图3.6　投资收益率R—累积概率P关系曲线

图3.6不仅仅反映了项目投资收益率的大小，同时也反映了小于等于某投资收益率的可能性的大小，它为合理决策提供了可靠依据。

5.结论

（1）本方法是以建设项目的经济评价指标投资收益率为例来说明风险元非线性传递通用模型的应用，对于其他评价指标如净效益现值、净现值率等均可用本方法来分析相应的风险。风险元非线性传递通用模型具有广阔的适用范围，凡是能表示成某些风险元的显函数表达式，并存在一阶连续偏导数，均可用风险元非线性传递通用模型来分析。

（2）风险元非线性传递通用模型同蒙特卡洛法一样考虑了各种风险元对目标值的综合影响，但风险元非线性传递通用模型是一种解析分析法，这是与蒙特卡洛模拟法的根本区别。与蒙特卡洛模拟法相比较该法具有如下优点：①解决了各个风险元之间的相互影响问题；②计算工作量小，不用编程即可完成较大项目的风险分析工作；③输入数据简单，不需要风险元的概率分布函数或概率密度函数，仅需反映概率分布的数字特征值（数学期望和方差）即可；④可以找出风险传递影响最大的关键风险元。

（3）风险元非线性传递通用模型采用概率分布统计特征参数来表征风险的传递，不能给出目标函数客观真实的概率分布，这是本方法的不足之处。但必须说明，由于每个风险元的分布均带有主观判断的成分，所以采用任何一种风险分析方法，都不可能给出目标函数的真实分布，只能是一种估计，由于一般的诸如经济评价指标等目标函数的影响因素较多，用正态分布来代替真实分布，误差很小，不致影响投资决策。